
Importer l’énergie solaire du désert ? Presque impossible…
Ne pourrait-on pas produire l’électricité avec des panneaux solaires déployés massivement dans le désert, et la distribuer ensuite dans les zones peuplées ? L’Europe pourrait par exemple faire produire via un partenariat économique toute son énergie solaire dans le désert, là où le soleil brille le plus fort et avec le moins de variations. En admettant que l’on dispose de moyens de stockage, ce projet se heurte de plein fouet à la quantité de matériaux et d’énergie qu’il faudrait mobiliser pour déployer l’infrastructure nécessaire au transport d’énergie.
De quelle énergie avons-nous besoin ?
Afin de déterminer les dimensions du réseau de transport d’électricité nécessaire, il faut tout d’abord déterminer la quantité que l’on souhaite faire produire dans le désert.
Energie par habitant
En Europe, la consommation moyenne d’électricité par habitant par an est de l’ordre de 6 MWh (=6 000 kWh). Cela couvre seulement un quart de la consommation totale d’énergie finale, qui s’élève à peu près à 24 MWh par habitant par an. Pour une transition énergétique réussie, il s’agit de produire l’intégralité de l’énergie finale utilisée avec des sources décarbonées, et pas uniquement l’énergie électrique produite actuellement. Cependant on est alors confrontés au fait de comparer des énergies de natures différentes. L’énergie électrique est de meilleure qualité que l’énergie thermique lorsqu’il s’agit de mettre en mouvement un moteur, car il s’agit d’une forme d’énergie potentielle. Par exemple le rendement d’un moteur électrique tourne autour de 80% tandis que les moteurs thermiques ne peuvent guère dépasser les 40%. Certes il faudrait prendre en compte les pertes lors du stockage/déstockage, mais il faudrait tout de même moins d’électricité si on électrifiait tous les transports.
S’il s’agit de remplacer le chauffage au gaz des habitations par des chauffages électriques, alors l’électricité n’est pas supérieure. En revanche on peut être plus malins et l’utiliser pour actionner des pompes à chaleur ce qui la rend alors trois fois plus intéressante. On peut donc dans un premier temps supposer que l’on pourrait remplacer les 18 MWh par habitant d’énergie finale non électrique par seulement 9 MWh d’électricité supplémentaire, portant le total d’énergie électrique à 15 MWh. En rajoutant quelques économies (certes rapidement ruinées lorsque l’on relocalisera notre industrie), et le fait qu’on pourrait quand même utiliser un peu d’énergie éolienne (là aussi limitée), un peu de biomasse, et un peu d’hydraulique, on peut raisonnablement considérer qu’il faudrait pouvoir produire 12 MWh d’énergie solaire par personne.
Il s’agit de toute façon d’une évaluation à la louche dépendant de choix technologiques pour le chauffage, les transports, et bien évidemment complètement dépendante de notre croissance ou décroissance économique accompagnant la transition. On retient ici simplement l’idée que pour se débarrasser entièrement des énergies fossiles, et même dans un scenario favorable, il faudrait produire avec de l’énergie solaire de l’ordre du double de toute l’électricité produite actuellement.
Par ailleurs, je me place volontairement dans un scenario où on ne déploierait pas le nucléaire de manière massive, puisqu’un tel projet de production dans le désert en serait précisément une alternative que l’on examine ici.
Puissance électrique solaire pour l’Europe
Avec ses 500 millions d’habitants, l’Union Européenne –à laquelle je n’ai pu m’empêcher d’ajouter le Royaume-Uni– aurait donc besoin de produire 6000 TWh d’énergie électrique solaire, soit en gros une puissance moyenne un peu inférieure à 700 GW.
Les parcs solaires ont en général une production moyenne par surface de l’ordre de 5 MW/km2 lorsqu’ils sont installés en France (éventuellement 6 MW/km2 dans le Sud-Est). On peut retrouver rapidement cet ordre de grandeur en prenant en compte l’ensoleillement, et l’efficacité des panneaux. En effet, la puissance moyenne d’irradiation solaire par surface en France, est de l’ordre de 120 W/m2. Avec une efficacité des panneaux de l’ordre de 15% cela ferait un production de 18W/m2 si les panneaux étaient collés les uns aux autres et placés sur le sol. En réalité ils sont orientés vers le soleil, mais espacés pour ne pas se faire de l’ombre et le résultat net théorique est une diminution par au moins deux de la puissance par surface de terrain. En conditions réelles, ce qui implique la prise en compte d’autre sources de pertes (comme la conversion en courant alternatif) on tombe en fait autour de 5 W/m2, ce qui est équivalent à 5 MW/km2.
Pour produire toute l’énergie solaire électrique nécessaire à l’Europe, il faudrait donc une surface de 140 000 km2. Ce n’est que 3% de la surface de l’Union Européenne, mais cela entrerait directement en concurrence avec d’autres usages. Il est donc légitime de savoir si on ne pourrait pas tout simplement utiliser cette même surface dans le désert, et transporter ensuite toute cette électricité via des lignes très haute tension. Il suffirait alors d’équiper moins de 2% de la surface du Sahara.
On va maintenant supposer que l’on dispose de moyens de stockage au plus près de la consommation (comme par exemple l’ensemble des batteries des véhicules électriques, et de nombreux autres moyens bien sûr). Il s’agit d’une hypothèse complètement irréaliste, mais on souhaite dans un premier temps séparer le problème du stockage de celui du transport de l’électricité.
Le transport de l’électricité
La puissance-distance
Une caractéristique centrale de l’énergie solaire est son intermittence. De manière théorique, en considérant une Terre sans nuage, il est impossible d’avoir un facteur de charge (le rapport entre la puissance moyenne et la puissance des pics de production) supérieur à 35%. En pratique, en prenant en compte les nuages, le facteur de charge est beaucoup plus faible, inférieur à 15% en France. L’avantage du désert est qu’on pourrait compter sur un facteur de charge un peu plus élevé, autour de 25% en étant très optimiste. La conséquence immédiate est qu’il faudrait surdimensionner l’infrastructure permettant d’acheminer l’électricité depuis le Sahara jusqu’en Europe. Avec une moyenne de 700 GW, il faudrait pouvoir transporter des pics de production de 2800 GW. Pour garder un chiffre rond, on retiendra le besoin de pouvoir transporter 3000 GW car il faut aussi prendre en compte que le processus de stockage/production d’électricité comporte également quelques pertes.
Pour résumer, en partant de la puissance moyenne électrique en Europe (autour de 350 GW), on considère qu’il faudrait pouvoir produire le double avec du solaire en moyenne (700 GW), et surdimensionner le réseau d’un facteur supérieur à 4 pour être capable de transporter des pics à 3000 GW.
Il faut ensuite déterminer sur quelle distance il faudrait acheminer une telle puissance. Pour cela il faut examiner une carte d’Europe, avec une idée approximative de la répartition de la population, pour imaginer ce à quoi un telle infrastructure pourrait ressembler. Il s’agit de réaliser une dorsale de transport (aussi appelée super grid) allant se raccorder sur quelques points aux réseaux très haute tension (THT) de chaque pays. Cette idée est résumée sur une le site de RTE
Construire les autoroutes de l’électricité à l’échelle européenne c’est permettre aux énergies renouvelables d’exprimer tout leur potentiel. Pour que le Nord profite du soleil du Sud et le Sud des vents du Nord. Ce qui suppose de construire des parcs éoliens offshore et de très longues lignes transeuropéennes Nord Sud auxquelles viendront se connecter les réseaux de chaque région d’Europe.
RTE: Au coeur des smartgrids en France et en Europe, l’intelligence sans frontière.
En voici une représentation schématique possible.

Source : Friends of the SuperGrid
En examinant cette carte, on estime rapidement qu’il faudrait transporter cette énergie sur une distance de 3000 km environ, soit la distance approximative entre les déserts d’Afrique du Nord et le centre de l’Allemagne. Un partie devrait être transportée sur des distances inférieures, notamment pour alimenter la péninsule ibérique, l’Italie ou la Grèce, et une partie à des distances supérieures pour alimenter le nord de l’Europe, et les Iles Britanniques. On peut le voir comme un ensemble de tuyaux qui partent du sud, et dont la taille ou le nombre diminue au fur et à mesure qu’ils remontent vers nord. Pour les besoins de l’estimation, on va donc considérer que l’on a besoin de transporter 3000 GW sur une distance de 3000 km.
On va voir qu’il est très utile d’introduire le concept de puissance-distance, qui est tout simplement le produit de la puissance à transporter par la distance sur laquelle il faut la transporter. La dorsale que nous envisageons doit donc avoir une puissance-distance de 9 000 000 GW.km.
Enfin dans notre évaluation je considère que l’énergie électrique éolienne reste marginale, mais si ça n’était pas le cas il faudrait certes transporter un puissance électrique solaire plus faible du sud vers le nord, mais il faudrait aussi prévoir le transport de l’énergie électrique éolienne intermittente du nord vers le sud. On ne pourrait alors pas se contenter d’un réseau dont le taille ou le nombre des tuyaux diminue du sud vers le nord. La distance effective de transport en serait d’autant plus rallongée, et la puissance-distance nécessaire pour la dorsale serait sensiblement la même.
Cette notion de puissance-distance est la bonne quantité pour évaluer la quantité de matériaux et l’énergie nécessaire pour construire cette dorsale. Pour voir cela, nous allons faire un petit détour vers les lignes très haute tension permettant de transporter de l’électricité sur de longues distances.
Les lignes THT en continu
En général les lignes haute tension, tout comme les lignes basse tension et le courant domestique, sont en courant électrique alternatif. Cependant, pour transporter de l’électricité sur de grandes distances cela pose plusieurs problèmes. La puissance transportée étant le produit de la tension et de l’intensité, l’intensité doit être maximale quand la tension est maximale, et nulle quand la tension est nulle. Ces deux quantités doivent alterner en même temps si on veut transporter correctement la puissance électrique. Sans rentrer dans les détails, (voir la vidéo du Réveilleur pour de nombreux détails), l’effet capacitif naturel des câbles tend à déphaser la tension de l’intensité, c’est à dire à faire en sorte que le maximum de l’intensité ne soit pas exactement en même temps que le maximum de tension, ce qui baisse la puissance transportée mais pas la puissance dissipée. Il faut donc placer régulièrement des dispositifs permettant de les remettre en phase et cela ajoute un coût supplémentaire, si bien que le transport en courant continu est moins cher sur de longues distances. Ensuite, si on connecte des réseaux alternatifs sur de très grandes distances, il faut veiller à leur synchronisation, c’est-à-dire au fait que la tension oscille à la même fréquence partout.
C’est pour ces raisons que le transport d’électricité sur de longues distances se fait préférentiellement avec des lignes à courant continu. Cela impose bien sûr de poser des convertisseurs du continu à l’alternatif et de l’alternatif au continu, mais le jeu en vaut la chandelle. Et cela tombe bien pour notre problème, puisqu’il est beaucoup plus simple d’expliquer comment les lignes à courant continu fonctionnent. Il suffit de se souvenir des travaux pratiques à l’école lors desquels on branchait des piles à des ampoules, et je sais de source sûre que cela se fait dès le CE2.
Une ligne de transport en courant continu est composée de deux fils. L’un à la tension ![]() et parcouru par un courant d’intensité
et parcouru par un courant d’intensité ![]() pour le trajet aller de l’électricité, et l’autre à la tension
pour le trajet aller de l’électricité, et l’autre à la tension ![]() et parcouru par un courant d’intensité
et parcouru par un courant d’intensité ![]() pour le trajet retour après transformation de l’énergie électrique en une autre forme d’énergie directement utile. L’ensemble de ces deux fils est appelé un bipôle. Dans chaque fil, la puissance transportée est
pour le trajet retour après transformation de l’énergie électrique en une autre forme d’énergie directement utile. L’ensemble de ces deux fils est appelé un bipôle. Dans chaque fil, la puissance transportée est
(1) ![]()
Par ailleurs, la puissance dissipée dans chaque fil est donnée par la célèbre formule
(2) ![]()
où ![]() est la résistance totale du fil. La résistance d’un fil dépend par ailleurs de sa forme et du matériau utilisé. La quantité qui caractérise la propension d’un matériau à résister au courant électrique s’appelle la résistivité et est notée
est la résistance totale du fil. La résistance d’un fil dépend par ailleurs de sa forme et du matériau utilisé. La quantité qui caractérise la propension d’un matériau à résister au courant électrique s’appelle la résistivité et est notée ![]() . Plus un fil est long, plus il sera résistant, et plus sa section est grande, moins il sera résistant. Imaginez-vous en train de marcher sur un sentier de randonnée. Plus il est long et plus vos souliers seront usés, et plus le sentier est large moins la randonnée est difficile. En accord avec ces idées simples, la formule générale donnant la résistance d’un fil en fonction de sa section
. Plus un fil est long, plus il sera résistant, et plus sa section est grande, moins il sera résistant. Imaginez-vous en train de marcher sur un sentier de randonnée. Plus il est long et plus vos souliers seront usés, et plus le sentier est large moins la randonnée est difficile. En accord avec ces idées simples, la formule générale donnant la résistance d’un fil en fonction de sa section ![]() et sa longueur
et sa longueur ![]() est
est
(3) ![]()
Bande passante
On peut remplacer la résistance par son expression (3) dans la formule de la puissance dissipée (2), et se débarrasser de l’intensité en l’exprimant en fonction de la puissance transportée (![]() ), pour obtenir une relation très instructive. On introduit pour cela le concept de fraction de pertes
), pour obtenir une relation très instructive. On introduit pour cela le concept de fraction de pertes ![]() comme étant le rapport entre la puissance dissipée et la puissance transportée, c’est-à-dire
comme étant le rapport entre la puissance dissipée et la puissance transportée, c’est-à-dire
(4) ![]()
Toute l’étude que l’on va faire suppose que ![]() est petit et on ne choisira jamais de valeur plus grande que
est petit et on ne choisira jamais de valeur plus grande que ![]() , c’est-à-dire des pertes de l’ordre de 10%. Cela revient à supposer que puissance produite puissance consommée sont à peu près égales. En théorie on pourrait très bien faire un calcul plus général en considérant la surproduction nécessaire pour compenser les pertes, mais cela ne ferait que compliquer les expressions de ce billet, et ne présenterait aucun intérêt pour la discussion puisque nous souhaitons évidemment limiter les pertes par dissipation. On obtient alors la relation centrale pour notre discussion :
, c’est-à-dire des pertes de l’ordre de 10%. Cela revient à supposer que puissance produite puissance consommée sont à peu près égales. En théorie on pourrait très bien faire un calcul plus général en considérant la surproduction nécessaire pour compenser les pertes, mais cela ne ferait que compliquer les expressions de ce billet, et ne présenterait aucun intérêt pour la discussion puisque nous souhaitons évidemment limiter les pertes par dissipation. On obtient alors la relation centrale pour notre discussion :
(5) ![]()
A gauche on a la puissance transportée multipliée par la longueur du fil. Il s’agit donc de la puissance-distance évoquée précédemment. Cette équation nous dit que cette puissance-distance est d’autant grande si :
- on accepte des pertes
 importantes,
importantes, - la tension
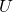 utilisée est élevée,
utilisée est élevée, - la section
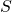 des fils est grande,
des fils est grande, - la résistivité
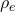 est faible.
est faible.
Par ailleurs, cette proportionnalité directe entre la puissance distance et la section du câble signifie qu’on peut soit considérer un seul câble géant, soit de multiples câbles de section plus petites. Par exemple si on considère 100 câbles, chacun de section 100 fois plus petite que le gros câble, la section totale dans laquelle l’électricité passe est la même. D’une certaine manière, on peut considérer qu’un gros câble est une multitude de petits câbles collés les uns aux autres (des résistances en parallèle), et c’est d’ailleurs assez proche du procédé de fabrication avec plusieurs sous-câbles torsadés. Si on cherche à déterminer la quantité de métal nécessaire à la réalisation de la dorsale, les détails du dispositif importent peu. Seule compte la puissance-distance, le matériau choisi, la tension utilisée, et les pertes que l’on trouvera acceptables, et cela déterminera de manière unique la section totale que l’on doit utiliser pour faire voyager les électrons. On obtient en effet à partir de (5)
(6) ![]()
En application de cette formule pour notre dorsale, on trouve qu’en utilisant du cuivre de résistivité ![]() , une puissance de 3000 GW, une distance de 3000 km, un taux de perte
, une puissance de 3000 GW, une distance de 3000 km, un taux de perte ![]() de 10%, et une tension
de 10%, et une tension ![]() (valeur admise pour de la très haute tension en continu moderne), la section requise serait alors de 6m2. Oui vous avez bien lu, 6 mètres carrés de section, ce n’est plus un fil mais un pipeline géant à électrons ! Mais c’est le minimum pour réaliser la dorsale car on ne pourrait accepter des pertes supérieures à 10%.
(valeur admise pour de la très haute tension en continu moderne), la section requise serait alors de 6m2. Oui vous avez bien lu, 6 mètres carrés de section, ce n’est plus un fil mais un pipeline géant à électrons ! Mais c’est le minimum pour réaliser la dorsale car on ne pourrait accepter des pertes supérieures à 10%.
On peut également utiliser (6) pour évaluer la taille d’une grosse ligne électrique très haute tension (500 kV) permettant de transporter 3 GW sur 3000 km avec 6% de pertes, et on trouve qu’il faudrait une section totale de 100cm2. C’est précisément le nec plus ultra du câble haute tension à courant continu, où l’on utilise 2 dipôles (soit 4 fils en tout), chacun de 25cm2 de section, portés à ![]() et parcourus par des courants de 1500A. On vérifie ainsi que la formule (5) reliant puissance-distance et section de câble est réaliste.
et parcourus par des courants de 1500A. On vérifie ainsi que la formule (5) reliant puissance-distance et section de câble est réaliste.
A noter que l’installation entre l’Espagne et la France récemment installée est constituée de tels câbles, mais portés à 320 kV seulement, et donc ne permettant de transporter que 2 GW. Elle a coûté, 700 millions d’euros pour 64 kilomètres, soit un peu plus de 10 millions d’euros au km. En admettant qu’on puisse l’utiliser avec du 500 kV pour la faire fonctionner à 3 GW, il nous faudrait la bagatelle 3 millions de kilomètres de ce type de ligne pour réaliser les 9 000 000 GW.km de la dorsale. Si le prix au kilomètre reste le même (bien sûr cela n’a pas de raison d’être le cas), cela va chercher dans les 3000 milliards d’euros. Une paille. Ce calcul financier ne vaut pas grand chose, mais permet de se rendre compte de l’ordre de grandeur des capitaux nécessaires.
Enfin, sachant que les interconnexions entre voisins Européens ne permettent jamais de faire passer plus que quelques GW, on mesure le défi de faire traverser une dorsale à travers l’Europe permettant de transporter 3000 GW sur une distance considérable.
Quel matériaux nécessaires ?
Des câbles en cuivre
Le coût financier évalué à la louche ci-dessus n’apporte aucune information sur la faisabilité. Les prix peuvent très bien s’écrouler lorsqu’une technologie est déployée de manière massive, ou au contraire s’envoler face à une limite physique liée à la raréfaction d’une ressource. Il est donc bien plus pertinent de regarder directement les quantités de matériaux et d’énergie mobilisés pour la construction.
La masse de métal utilisée est proportionnelle à la masse volumique ![]() du métal (9 tonnes par mètre cube pour du cuivre), et au volume de métal, lui même donné par le produit de la longueur et de la section, c’est-à-dire
du métal (9 tonnes par mètre cube pour du cuivre), et au volume de métal, lui même donné par le produit de la longueur et de la section, c’est-à-dire ![]() . Avec l’expression (6) pour la section, on en déduit alors une relation éclairante permettant de déterminer la masse de métal nécessaire en fonction des caractéristiques de la dorsale :
. Avec l’expression (6) pour la section, on en déduit alors une relation éclairante permettant de déterminer la masse de métal nécessaire en fonction des caractéristiques de la dorsale :
(7) ![]()
Chaque facteur de cette expression peut se comprendre facilement.
- Plus le métal est résistant, et plus il en faut un grand volume pour éviter les pertes de dissipation, d’où le facteur
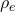 .
. - Plus le métal est dense et plus cela se traduit par une masse élevée, d’où le facteur multiplicatif
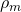 .
. - Plus on veut transporter de puissance, et il plus il faut de métal, d’où le facteur
 .
. - Quant au facteur
 il vient du fait que la masse est proportionnelle à la longueur, et la section également si on souhaite viser un certain taux de pertes
il vient du fait que la masse est proportionnelle à la longueur, et la section également si on souhaite viser un certain taux de pertes  .
. - Plus le taux de pertes visé est faible, et plus il faut de métal, d’où le facteur
 au dénominateur.
au dénominateur. - Enfin plus on utilise de la haute tension, et plus on réduit les pertes dissipatives et donc moins on a besoin de métal, d’où le facteur
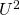 au dénominateur. Le fait qu’on divise par le carré de la tension et non uniquement par la tension est la seule caractéristique peu intuitive dans la relation (7).
au dénominateur. Le fait qu’on divise par le carré de la tension et non uniquement par la tension est la seule caractéristique peu intuitive dans la relation (7).
En application de cette formule pour notre dorsale, on trouve qu’il faudrait 165 millions de tonnes de cuivre. Dans cette installation, chaque GW.km de puissance-distance nécessite 18 tonnes de cuivre, et comme il nous faut 15 millions de GW.km, cela se traduit par des quantités astronomiques de métal. Remarquons par ailleurs qu’un bon câble permettant normalement de ne faire circuler que 0.75 GW (très haute tension de 500 kV et courant de 1500 A), fait 25cm2 de diamètre, ce qui fait 22 tonnes par km, et ferait environ 30 tonnes par kilomètre si on l’agrandissait pour y faire passer 1GW. Si nous avons obtenu ce chiffre de 18 tonnes de cuivre par km pour faire passer 1GW, c’est uniquement parce que nous avons accepté 10% de pertes sur notre dorsale, ce qui est en dessous des standards actuels.
Pour se rendre compte de ce que signifient les 165 millions de tonnes de cuivre pour réaliser notre dorsale de piètre qualité, il faut comparer avec la production annuelle de cuivre qui est de 20 millions de tonnes. On imaginant que l’Europe se taille la part du lion et en capte 10%, soit plus que sa part de population mondiale, cela ne ferait que 2 millions de tonnes par an, et il faudrait 82 années pour disposer du cuivre nécessaire, en ne l’utilisant d’ailleurs pas pour d’autre usages. C’est donc parfaitement impossible. D’ailleurs, les réserves mondiales de cuivre sont estimées autour de 600 millions de tonnes. En estimant que l’Europe peut en capter 10%, soit 60 millions de tonnes, il est clair que le cuivre manquera très largement. Construire une dorsale permettant d’alimenter l’Europe avec l’énergie solaire du désert est donc impossible avec des câbles en cuivre.
L’aluminium à la rescousse
Si dans le titre j’ai écrit presque impossible, et non pas impossible, c’est précisément parce qu’il existe une alternative crédible au cuivre. En effet, on peut parfaitement utiliser de l’aluminium dont la résistivité n’est que 64% plus élevée que celle du cuivre (![]() ), et nettement plus abondant sur Terre. En théorie l’or et l’argent ont des propriétés conductrices aussi bonnes que le cuivre, mais on se doute bien qu’ils sont encore largement moins abondants, si bien que l’aluminium est le métal le plus évident pour fabriquer des câbles après le cuivre.
), et nettement plus abondant sur Terre. En théorie l’or et l’argent ont des propriétés conductrices aussi bonnes que le cuivre, mais on se doute bien qu’ils sont encore largement moins abondants, si bien que l’aluminium est le métal le plus évident pour fabriquer des câbles après le cuivre.
Etant plus résistif, on constate directement avec la relation (6) que les sections nécessaires doivent être augmentées de 64%. Pour notre dorsale, il faudrait donc une section totale de 10m2. Cependant l’aluminium est beaucoup plus léger (2.7 tonnes par mètre cube). La relation (7) montre en effet clairement qu’il faut prendre en compte le produit de la résistivité par la masse volumique pour déterminer la masse nécessaire. L’aluminium conduit moins bien que le cuivre, mais il est si léger qu’au final il en faudrait quand même deux fois moins (en masse) que de cuivre. Une manière d’écrire 7 pour l’aluminium est
(8) ![]()
avec ![]() en millions de tonnes, la puissance
en millions de tonnes, la puissance ![]() en
en ![]() (
(![]() ), la longueur
), la longueur ![]() en kilomètres, la tension
en kilomètres, la tension ![]() en
en ![]() , et enfin la fraction de pertes
, et enfin la fraction de pertes ![]() en pourcentages. Pour notre dorsale de 3000km, en 500kV, passant 3TW avec 10% de pertes, cette formule indique qu’il suffirait en théorie de l’ordre de 80 millions de tonnes d’aluminium, soit effectivement la moitié de ce qu’il aurait fallu en utilisant du cuivre.
en pourcentages. Pour notre dorsale de 3000km, en 500kV, passant 3TW avec 10% de pertes, cette formule indique qu’il suffirait en théorie de l’ordre de 80 millions de tonnes d’aluminium, soit effectivement la moitié de ce qu’il aurait fallu en utilisant du cuivre.
Avec des réserves autour de 6000 millions de tonnes et une production annuelle de 60 millions de tonnes, on pourrait être tenté de penser que cet objectif est accessible. Si l’Europe utilise 10% de cette production, et en consacre la moitié uniquement à cet usage (soit donc 3 millions de tonnes par an) cela nécessiterait au moins 27 ans pour y arriver. Au vu de l’urgence de décarboner nos économies c’est déjà trop long, et RTE souhaiterait que le déploiement d’une dorsale se fasse en 10 ans. Il faudrait donc tripler la production d’aluminium afin d’accélérer la construction. C’est difficile mais cela reste envisageable. Cependant, il y a de nombreuses autre difficultés qui viennent s’ajouter, rendant l’objectif presque impossible à atteindre.
Surdimensionner le réseau national
Tout d’abord nous avons seulement estimé la quantité d’aluminium pour la dorsale. Mais si on décide que les moyens de stockage sont en bout de réseau, par exemple chez les particuliers et les entreprises, alors il faut également surdimensionner les réseaux haute et moyenne tension nationaux ainsi que les boucles finales de basse tension.
La masse supplémentaire doit encore être évaluée avec la relation (8), sur laquelle on remarque une dépendance en ![]() . Cette expression doit être appliquée à chaque partie du réseau, à savoir la partie haute tension, la partie moyenne tension, et la partie basse tension.
. Cette expression doit être appliquée à chaque partie du réseau, à savoir la partie haute tension, la partie moyenne tension, et la partie basse tension.
- Pour la partie haute tension, l’électricité est typiquement transportée sur 500 km, et avec une tension de 400 kV. Certes il s’agit de courant alternatif, mais cette tension est la tension équivalente en continu, et on peut donc faire les raisonnements comme s’il s’agissait de courant continu (merci à des lecteurs attentifs pour cette remarque). Par rapport à la dorsale, on a donc une longueur 6 fois plus petite, mais une tension à peine plus basse. Le facteur
 est donc environ 20 fois plus petit. Même si on augmente les sections d’un facteur 4 (pour avoir des pertes plafonnées à 2.5% (plutôt que les 10% pour la dorsale), la masse de métal mobilisée pour la partie haute tension est de l’ordre de 20% de celle utilisée pour construire la dorsale.
est donc environ 20 fois plus petit. Même si on augmente les sections d’un facteur 4 (pour avoir des pertes plafonnées à 2.5% (plutôt que les 10% pour la dorsale), la masse de métal mobilisée pour la partie haute tension est de l’ordre de 20% de celle utilisée pour construire la dorsale. - On peut refaire le même raisonnement pour la moyenne tension. Je simplifie un peu car la tension est normalement abaissée progressivement de 400 kV à 20 kV en passant par 225 kV puis 90 kV. Je suppose que l’on a une desserte régionale à 20 kV (tension alternative équivalent à 14 kV en continu) sur une longueur typique de 50 km. La distance est donc 60 fois plus petite que pour la dorsale, et la tension est 25 fois plus basse. Encore une fois le facteur
 est donc autour de 9 fois plus petit que pour la dorsale. Si on vise des pertes plafonnées à 2.5% au lieu de 10% sur cette partie du réseau, il faudrait augmenter les sections d’autant si bien que la masse nécessaire pour la partie moyenne tension serait de l’ordre de la moitié de celle utilisée pour la dorsale.
est donc autour de 9 fois plus petit que pour la dorsale. Si on vise des pertes plafonnées à 2.5% au lieu de 10% sur cette partie du réseau, il faudrait augmenter les sections d’autant si bien que la masse nécessaire pour la partie moyenne tension serait de l’ordre de la moitié de celle utilisée pour la dorsale. - Enfin on arrive à la boucle locale. Il s’agit de 230 V alternatif, soit une tension environ 2000 fois plus basse que pour la dorsale. Cependant la longueur de la boucle locale ne peut raisonnablement pas être inférieure au kilomètre, ce qui est la taille d’une petite ville ou d’un quartier. La longueur moyenne serait donc 3000 fois plus petite que notre dorsale. Le facteur
 serait de l’ordre de deux fois celui utilisé pour la dorsale ! Si en plus on souhaite limiter les pertes à un pourcentage sensiblement plus petit que 10%, il va donc bien falloir plusieurs fois la masse calculée pour la dorsale rien que pour cette boucle finale. La boucle locale n’étant pas en haute tension, elle ruine une bonne partie des efforts faits pour éviter les pertes dissipatives…
serait de l’ordre de deux fois celui utilisé pour la dorsale ! Si en plus on souhaite limiter les pertes à un pourcentage sensiblement plus petit que 10%, il va donc bien falloir plusieurs fois la masse calculée pour la dorsale rien que pour cette boucle finale. La boucle locale n’étant pas en haute tension, elle ruine une bonne partie des efforts faits pour éviter les pertes dissipatives…
En additionnant tout, il faudrait bien, au doigt mouillé, 5 fois plus de métal que pour la dorsale seule. Ici il s’agit vraiment d’une évaluation en ordre de grandeur, mais elle nous fait tomber sur un chiffre qui tourne autour de 400 millions de tonnes d’aluminium. Avec 10% de la production mondiale uniquement pour cet usage, il faudrait tout de même autour de 65 ans pour produire l’aluminium nécessaire. Cependant, même si les réserves d’aluminium sont très grandes, elles sont estimées à 6000 millions de tonnes. Si l’Europe s’en arroge 10%, il faudrait qu’elle en consacre quasiment tout à développer son système de transport d’électricité.
Réduire l’intermittence
Jusqu’ici, nous avons eu besoin de surdimensionner le réseau, car nous avons supposé que les moyens de stockage sont en bout du réseau de distribution. Si le stockage/production se fait au niveau du désert, la source d’énergie n’est plus intermittente et il n’y a plus lieu de surdimensionner d’un facteur 4 le réseau.
La méthode la plus évidente pour réduire l’intermittence avec l’énergie solaire consiste à utiliser des centrales à concentration permettant de stocker l’excès thermique de la journée pour le réutiliser la nuit. L’intermittence de ce moyen de production se réduirait encore aux variations saisonnières.
Cependant, en allant chercher l’énergie solaire jusque dans la zone intertropicale où les différences entre les saisons sont faibles, on pourrait donc avoir une source d’énergie à peu près constante, mais cela impliquerait d’allonger la dorsale. Chaque degré de latitude correspond à une distance de 110 km. Si on descend à 15 degrés de latitude au lieu de 35 degrés pour implanter les usines solaires à concentration, il faudrait allonger la dorsale d’environ 2500 km. Au final la puissance-distance de la dorsale ne serait pas divisée par 4 mais plutôt par 2 par rapport au calcul effectué plus haut. En revanche la puissance-distance des réseaux nationaux de haute, moyenne et basse tension pourraient bien être divisée par 4 par rapport au cas complètement intermittent envisagé précédemment.
En prenant tout cela en compte, on pourrait alors s’en sortir avec « seulement » 100 millions de tonnes d’aluminium. Encore une fois, en considérant que l’Europe peut compter sur 10% de la production mondiale, et en utilisant la moitié (car il faudrait garder un grande quantité d’aluminium pour d’autres usages), cela prendrait 33 ans, ce qui est beaucoup trop long par rapport à l’urgence du problème climatique. Bien évidemment, il faudrait alors envisager la possibilité d’augmenter très fortement la production d’aluminium pour réduire drastiquement ce délai.
A vrai dire, étant données toutes les incertitudes liés à l’intermittence, au stockage, à la consommation future, il est vain de chercher à déterminer un chiffre précis pour la quantité d’aluminium nécessaire pour adapter notre système de distribution d’électricité. On retient simplement que cela sera complètement impossible avec du cuivre, et que si on utilise de l’aluminium il faudrait entre une centaine de millions de tonnes dans une estimation basse, à quelques centaines, disons 400 pour fixer les idées, dans une estimation haute.
Quelle énergie pour fabriquer ce réseau ?
L’aluminium est un métal dont la production est très énergivore. C’est d’ailleurs pour cela qu’historiquement les usines ont été placées au plus près des lacs de barrages, afin d’utiliser directement l’électricité hydroélectrique. Il est alors légitime de se poser la question de la possibilité de produire une telle quantité d’aluminium.
Pour passer de l’alumine (un oxyde d’aluminium présent dans la bauxite) à l’aluminium métallique, il faut passer par une étape d’électrolyse qui consomme une grande quantité d’électricité. De manière théorique il faut au minimum 5.6 MWh pour l’étape d’électrolyse nécessaire à la fabrication d’une tonne d’aluminium. En pratique il y a de nombreuses pertes difficilement évitables, si bien que le procédé nécessite autour de 15 MWh (soit environ 60 GJ) par tonne d’aluminium.
De plus, il faut aussi prendre en compte l’énergie nécessaire pour la fabrication des produits chimiques nécessaires à cette électrolyse, ainsi que la fabrication des cathodes et des anodes. Et ce n’est pas la seule étape qui consomme de l’énergie dans le procédé de fabrication. Il faut rajouter l’énergie pour l’extraction minière, le transport et les nombreuses autres étapes du procédé. Norgate et Rankin ont évalué que l’énergie totale dépensée pour une tonne d’aluminium se situe autour de 210 GJ par tonne d’aluminium. Bien évidemment, faire l’évaluation de l’énergie totale est complexe et va dépendre des détails du processus de fabrication, et même de la pureté du minerai initial. Chaque étude fournit donc un chiffre différent. Pour plus de détails sur les nombreuses incertitudes affectant ces estimations, je vous recommande la lecture de « Quel avenir pour les métaux« .
En retenant ce chiffre de 210 GJ (soit 60 MWh) par tonne d’aluminium, on peut estimer facilement l’énergie nécessaire pour la dorsale et l’adaptation du réseau. Dans l’hypothèse basse, il faut 6000 TWh pour fabriquer les 100 millions de tonnes d’aluminium. Dans l’hypothèse haute, il faut 24 000 TWh pour fabriquer les 400 millions de tonnes d’aluminium.
Pour se rendre compte à quel point c’est gigantesque, on peut comparer avec la production totale d’électricité en Europe, qui est de l’ordre de 3000 TWh par an. En mobilisant 10% de l’électricité produite, cela prendrait 20 ans dans l’hypothèse basse et 4 fois plus longtemps dans l’hypothèse haute.
Une autre façon de mettre en perspective ces chiffres consiste à les rapprocher de l’énergie utilisée pour la métallurgie. Actuellement, environ 10% de l’énergie primaire est consommée par la métallurgie. La grande majorité correspond à la fabrication d’acier, mais le quart est utilisé pour la fabrication d’aluminium. Si on devait augmenter considérablement la production d’aluminium, cela signifierait des besoins très fortement accrus pour ce secteur économique, et ce même dans l’hypothèse basse. Quant à l’hypothèse haute, cela représenterait bien plus qu’un effort de guerre.
Il est donc clair qu’une grande partie de l’augmentation de production d’électricité devra être affectée directement à cet effet. Nous devrions donc à la fois augmenter très largement la production d’électricité pour remplacer les énergies fossiles, mais également pour pouvoir fabriquer le réseau nécessaire à l’acheminement de cette augmentation d’électricité.
Conclusion
Pour résumer, soit nous n’aurions pas assez de cuivre pour réaliser un réseau permettant d’importer massivement de l’énergie solaire du sud, ou de l’éolien du nord, soit il nous faudrait une quantité d’énergie faramineuse pour fabriquer l’aluminium nécessaire. Cela n’est certes pas totalement impossible, mais presque impossible. Car lors de cette estimation, nous n’avons pas compté l’énergie nécessaire à la fabrication des câbles à partir de l’aluminium, la fabrication des pylônes et leur pose, le creusement des tunnels si on enterre les lignes. Cela n’inclut pas non plus l’énergie ni les matériaux nécessaires pour les connecteurs et transformateurs, plus la construction des moyens de stockage et de production d’électricité solaire.
On pourrait éventuellement revoir fortement à la baisse nos besoins énergétiques, auquel cas toutes les estimations en seraient réduites d’autant. Mais étant donné le lien étroit entre énergie et PIB, cela impliquerait une décroissance non négligeable.
Comme le résume très bien RTE, avant de fabriquer les supergrids il ne faudrait pas « oublier la faisabilité […] de chaque hypothèse ». En effet… sauf si comme RTE on vend le rêve d’un monde sans « frontière pour les électrons » !
Si vous avez aimé ce billet, partagez-le, notamment sur les réseaux sociaux avec les boutons ci-dessous. Et pour recevoir une notification à chaque nouveau billet, vous pouvez vous abonner avec votre adresse mail sur la colonne à droite.
Suivez-moi aussi sur Twitter : @CyrilPitrou
Image par analogicus de Pixabay

Approche très pertinente du problème. Mais en faisant abstraction des difficultés inhérentes à la situation du Sahara : sabotages et chantages toujours possibles ; pressions politiques des gouvernements locaux… Ne pourrait-on imaginer une solution basée sur l’hydrogène ? On pourrait au bord du rivage sud de la Méditerranée construire des électrolyseurs qui permettraient d’obtenir de l’hydrogène qui liquéfié (problème de la très basse température de liquéfaction) serait ensuite transporté par bateau vers des ports auprès desquels seraient édifiées des centrales de conversion ?