Pourra-t-on voyager vers une autre étoile ?

Pourra-t-on voyager vers une autre étoile ?

24 février 2023 Non Par Cyril Pitrou

De tous temps les hommes1 ont cherché à explorer leur environnement, par curiosité bien sûr, mais également pour l’occuper, et bien évidemment pour en utiliser les ressources. Les territoires connus correspondaient à ce qui avait été parcouru. Découvrir la Terre, c’était avant tout l’explorer. Puis avec des outils permettant de voir loin, on a pu observer et donc découvrir l’Univers au-delà de notre seule planète, sans forcément l’explorer.

Le décalage entre ce qui peut être exploré et ce qui peut être observé n’a fait que grandir. Les humains ont à peine atteint les confins du système solaire, et c’est en comptant l’envoi de sondes spatiales, car sans cela ils n’ont pas dépassé la Lune, située à environ une seconde-lumière. Or on sait désormais que notre système solaire se situe au sein d’une galaxie comportant des centaines de milliers d’étoiles, et cette galaxie est elle-même une simple galaxie dans un océan de galaxies.

On comprend désormais même la structure à grande échelle de l’Univers, et on sait que son expansion cosmologique pose une limite à ce qu’on peut observer. Même avec les meilleurs télescopes du monde, on ne saura jamais ce qu’il y a au-delà ce cette portion de l’espace qu’on appelle l’Univers observable et dont les dimensions se comptent en quelques milliers de milliards d’années-lumière. Il s’agit d’un exemple emblématique où la science peut affirmer qu’elle sait qu’on ne saura pas pour des raisons fondamentales.

Mais que nous dit la science sur ce qu’on pourra un jour explorer avec des vaisseaux spatiaux ? Sera-t-on capable d’aller visiter nos étoiles voisines afin de disposer de nouvelles ressources ? Quel serait le meilleur moteur possible ? Et quelle serait sa masse par rapport à celle de la capsule ? Combien de temps prendrait un voyage spatial vers une autre étoile ? Nous allons explorer ces trois dernières questions pour comprendre les limitations fondamentales des voyages spatiaux.

Les fusées du futur

La fusée idéale

Un vaisseau spatial, c’est une capsule permettant d’y vivre, mais également un système de propulsion. Puisque l’on cherche à comprendre les limites fondamentales au transport interstellaire, il nous faut envisager un progrès technique fabuleux permettant d’optimiser tout ce qui peut l’être. On peut donc considérer que le moteur est infiniment léger, c’est-à-dire que sa masse est complètement négligeable devant celle du carburant utilisé. De même la masse de ce qui permet de stocker le carburant sera tellement optimisée qu’elle pourra être ignorée.

La fusée idéalisée est donc constituée d’une capsule, habitée ou non, et de carburant qui peut être consommé pour éjecter des gaz servant à la propulsion par réaction. La masse initiale est donc celle de la capsule et du carburant, et une fois que ce dernier a été consommé, il ne reste plus que la capsule. Pour cette fusée idéalisée, il n’y a donc pas besoin de considérer divers étages dont on se débarrasserait comme dans une fusée classique. Même avec tous ces progrès hypothétiques et irréalistes, la performance de cette fusée idéalisée dépend nécessairement de la nature du système de propulsion et donc de l’énergie utilisée

Énergie chimique

Les fusées actuelles utilisent l’énergie chimique présente dans le carburant. Une méthode consiste simplement à utiliser la réaction entre le dioxygène et le dihydrogène pour former de l’eau. Ces réactifs peuvent être obtenus par la réaction inverse d’hydrolyse de l’eau qui nécessite de consommer de l’énergie électrique. Cependant l’énergie chimique libérée est toujours très faible au regard de l’énergie totale disponible.

L’énergie totale disponible pour n’importe quel type de matière est liée à la masse selon la célèbre formule E = m c^2, avec c \simeq 300000km/s la vitesse de la lumière. Ainsi 1kg de matière au repos correspond à une énergie de E_{1 {\rm kg}} = 1 \times (3\times 10^8)^2 J = 9\times 10^{16} J, soit environ 100 milliards de mégajoules. Cependant la réaction de 1kg de dihydrogène et de dioxygène dans les bonnes proportions, ne pourra fournir qu’environ 14 mégajoules.

D’une manière générale, tous les propergols utilisés dans les fusées permettent d’obtenir environ 10 mégajoules d’énergie chimique. Les réactions chimiques ne permettent donc d’obtenir que 10^{-10} de toute l’énergie disponible, soit un dix-milliardième. 1kg de dihydrogène et d’oxygène dans les bonnes proportions, ne permet pas de produire 1kg d’eau, mais 0.9999999999kg d’eau. C’est cette infime différence de masse, convertie en énergie cinétique de la vapeur expulsée, qui est utilisée pour pousser la fusée par réaction !

Énergie nucléaire

On peut certainement faire mieux. Plutôt que de récupérer l’énergie de liaison chimique qui correspond à une proportion infime de la masse totale, on peut récupérer l’énergie de liaison nucléaire des noyaux atomiques. L’énergie de liaison varie selon les éléments. Comme le montre la courbe d’Aston dans la figure suivante, elle croît pour les éléments légers jusqu’à atteindre un maximum pour le Fer, puis au-delà, pour les atomes plus gros que le Fer, elle décroît graduellement.

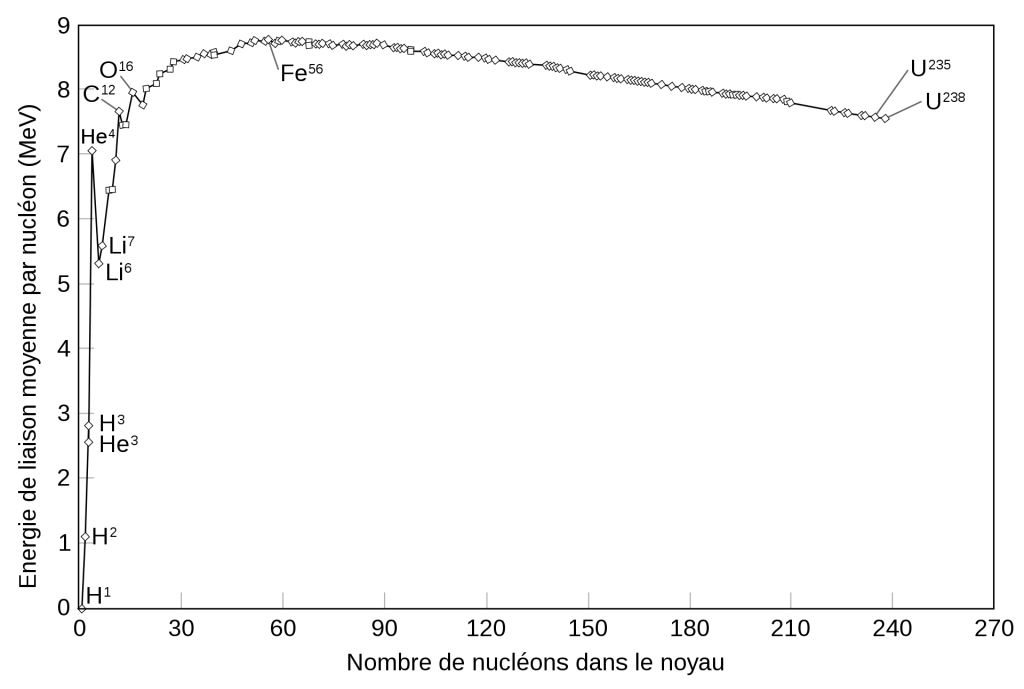
Énergie de liaison en fonction de la taille du noyau (nombre de nucléons).
Source : Wikipedia, Wikimedia Commons, Fastfission.

Pour récupérer l’énergie de liaison nucléaire, on peut donc soit fusionner des éléments légers, soit fissionner des éléments lourds. La fission de l’uranium 235 permet de récupérer une énergie d’environ 0.1% de toute l’énergie de masse2, tandis que la fusion de noyaux très légers permet de récupérer de l’ordre de 1% de toute l’énergie de masse2. L’énergie nucléaire est donc une source d’énergie beaucoup plus performante que l’énergie chimique, et si on maîtrise déjà la fission nucléaire comme source d’énergie, on comprend l’espoir que suscite la fusion nucléaire étant donnée l’abondance de l’hydrogène.

Énergie d’annihilation

Comme nous le verrons plus bas, même un réacteur à fusion nucléaire ne suffirait pas, et récupérer 1% de toute l’énergie disponible dans la matière est encore bien trop médiocre. Cependant aller au delà semble quasiment impossible. Les premiers travaux sur les propulsions du futur datent à ma connaissance d’un article de Ackeret en 1946, Zur Theorie der Raketen, et déjà dans les rêves les plus fous cela semblait impossible. En effet, pour récupérer toute l’énergie il ne faudrait produire que des photons sans masse.

Dès 1950 Eugene Sänger avait étudié brièvement les limites que nous allons discuter plus bas dans ce cas relevant de la science-fiction. Cependant il faudrait être capable de diriger tous ces photons dans la même direction pour utiliser le principe de réaction. Or tout dispositif tentant de le faire serait irrémédiablement désintégré par des photons aussi énergétiques. Une méthode consistant à produire uniquement des photons pas annihilation d’électrons et positrons est totalement impossible fondamentalement, pour de multiple raisons détaillés par Semyonov (2014).

D’après un article d’Ulrich Walter de 2006, le mieux que l’on puisse faire serait d’utiliser la réaction d’annihilation de protons et d’antiprotons. Cela produit en partie des particules chargées qu’on peut espérer rediriger dans la bonne direction avec des champs magnétiques. De manière effective, cela revient à récupérer 2% de toute l’énergie de masse du carburant6. C’est toujours mieux que les 1% de la fusion nucléaire, mais tellement loin d’une source d’énergie parfaite qui récupérerait 100% de l’énergie de masse du carburant.

De plus, il faut souligner que les difficultés techniques d’un tel dispositif sont titanesques et font passer la fusion nucléaire pour un jeu d’enfant. Comment stocker des antiparticules et des particules sans que tout cela dégénère en une immense explosion d’annihilation non contrôlée ? Par ailleurs, une partie de l’énergie produite l’est sous forme de photons dont l’énergie disloquerait instantanément toute forme de matière qu’elle rencontrerait. Il serait donc impossible de concevoir un moteur et une capsule qui y résisteraient.

Vitesse d’éjection

Oublions toutes ces difficultés un instant et imaginons que cela soit tout de même possible. Nous pouvons donc envisager quatre catégories de propulsion dont nous connaissons la fraction \epsilon d’énergie récupérable pour la propulsion :

  • La propulsion à énergie chimique (maîtrisée), \epsilon \simeq 10^{-10} ;
  • La propulsion à énergie de fusion nucléaire, \epsilon \simeq 0.01;
  • La propulsion à énergie d’annihilation, \epsilon \simeq 0.02;
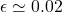  • La propulsion parfaite à photons (impossible), \epsilon = 1.

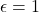Quelles seraient les vitesses des gaz éjectés dans ces trois scenarios ? Dans un cas de moteur idéal ne propulsant que de la matière, une formule simple permet de relier la fraction d’énergie récupérée \epsilon à la vitesse d’éjection3 v_e :

(1)   \begin{equation*}v_e = c \sqrt{2 \epsilon - \epsilon^2}\,.\end{equation*}

Les moteurs utilisant l’énergie de liaison chimique, comme ceux fonctionnant avec un mélange hydrogène-oxygène, ne produisent que des vitesses légèrement supérieures à 10^{-5} de celle de la lumière, soit environ 4km/s. Le moteur à fusion nucléaire permettrait d’atteindre une vitesse d’éjection à 14% de celle de la lumière, tandis que le moteur de science-fiction à annihilation pousserait ses gaz à 20% de la vitesse de la lumière6, comme on peut le voir sur la figure suivante dans laquelle une échelle logarithmique permet de visualiser sur le même graphique des moteurs aux performances théoriques immensément différentes.

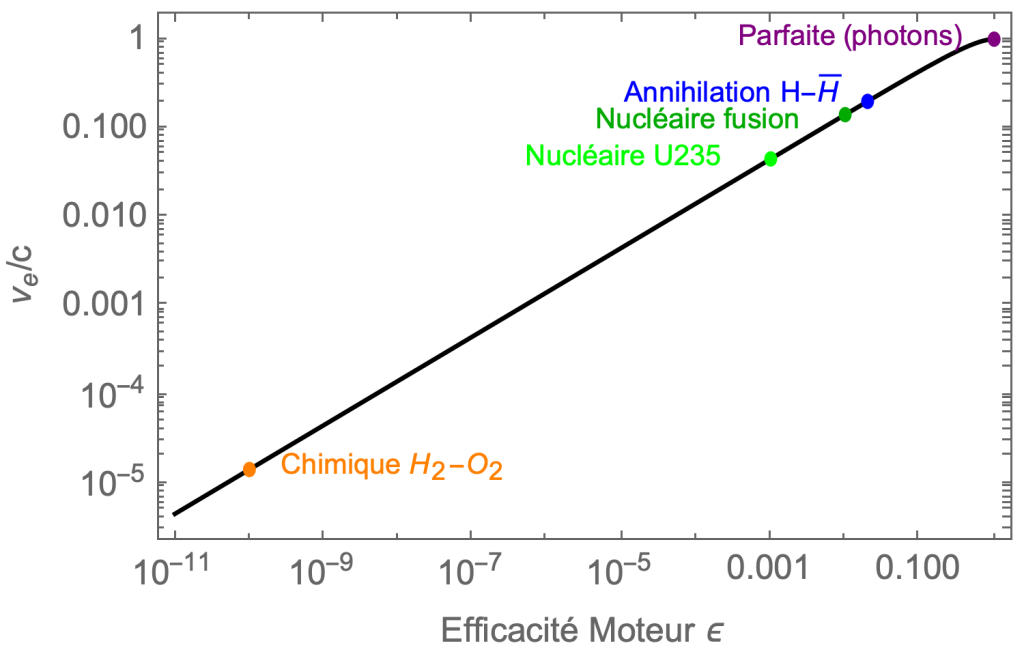
Vitesse d’éjection en fonction de la fraction de masse \epsilon convertie en énergie. La vitesse d’éjection est exprimée en unité de vitesse de la lumière, et ne peut donc excéder 1. Cette vitesse d’éjection maximale est atteinte lorsque toute la masse du carburant est convertie en énergie, ce qui correspond à \epsilon=1 en haut à droite de la courbe.
Source : de l’auteur.

Vitesse finale

En sachant la vitesse d’éjection des gaz, on souhaite maintenant déterminer jusqu’à quelle vitesse cela permettra d’accélérer la capsule. Bien évidemment cela va dépendre de la quantité de carburant utilisée. Plus généralement, on peut montrer que le rapport entre la masse totale initiale (capsule et carburant) et la masse finale (capsule seule) est le paramètre crucial. On notera ce rapport M_{\rm initiale}/M_{\rm finale}.

Pour fixer des ordres de grandeur, la charge utile sur Ariane 5 est de 10 tonnes alors que la masse totale de la fusée au décollage est de 750 tonnes. La charge utile sur les missions Apollo était d’environ 50 tonnes, alors que la fusée Saturn V avait une masse d’environ 3000 tonnes. Il est donc courant d’avoir de l’ordre de 100 fois plus de masse initiale que de masse utile (la masse finale). Pour lancer la sonde New Horizons qui a survolé de près Pluton, et dont la masse est d’environ 500 kg, on a utilisé une fusée Atlas de plus de 500 tonnes, soit 1000 fois plus massive ! Si on se place dans le vide, quelle vitesse peut-on atteindre pour un certain ratio M_{\rm initiale}/M_{\rm finale} ?

Si les vitesses atteintes son très inférieures à celle de la lumière, une formule bien connue, l’équation de Tsiolkovski, permet de relier ce ratio M_{\rm initiale}/M_{\rm finale}, à la vitesse d’éjection v_e, et la vitesse obtenue par la charge utile v_{\rm finale}. En revanche lorsque l’on commence à s’approcher de la vitesse de la lumière il faut modifier cette formule pour prendre en compte les effets relativistes, qui garantissent que la vitesse de la lumière n’est jamais dépassée. Ce qui suit est volontairement plus technique. Cependant il n’est pas nécessaire de comprendre les équations puisqu’elles sont traduites plus bas sous forme de graphe.

En ne prenant en compte que la physique classique4, la vitesse finale s’exprime simplement par l’équation de Tsiolkovski :

(2)   \begin{equation*}v_{\rm finale} = v_e \ln (M_{\rm initiale}/M_{\rm finale})\,.\end{equation*}

Pour certains la présence du symbole \ln, le logarithme naturel, semblera barbare. Sa présence a pourtant une explication intuitive. Elle signifie que multiplier par 10 la masse initiale ne permettra absolument pas d’atteindre une vitesse finale de capsule 10 fois plus élevée. En effet, une fusée doit accélérer à la fois le carburant utilisé ultérieurement et la charge utile. Rajouter du carburant, c’est également rajouter de la masse qu’il faudra accélérer. Il s’agit de la grande malédiction des fusées qui se traduit par l’écrasement impitoyable du logarithme.

Si on s’approche de la vitesse de la lumière cette formule n’est plus valable. Il faut la remplacer par la version relativiste5 :

(3)   \begin{equation*}v_{\rm finale} = v_e \left( \frac{\alpha -1}{\alpha+1}\right),\qquad \alpha \equiv \left(\frac{M_{\rm initiale}}{M_{\rm finale}}\right)^{2 v_e/c}\,.\end{equation*}

Sur les figures ci-dessous, on a tracé la vitesse finale de la capsule (en unité de la vitesse de la lumière), en fonction du rapport des masses, dans les cas de la physique classique et de la physique relativiste. Si la courbe classique paraît linéaire, ce n’est dû qu’à la présence d’une échelle logarithmique en abscisse. De plus elle permet d’atteindre des vitesses plus élevées que celle de la lumière et ne peut donc clairement pas être correcte. Cela montre bien l’intérêt de considérer la formule relativiste (3) qui écrase encore plus la vitesse finale pour l’empêcher de dépasser celle de la lumière, quelle que soit la masse initiale de la fusée.

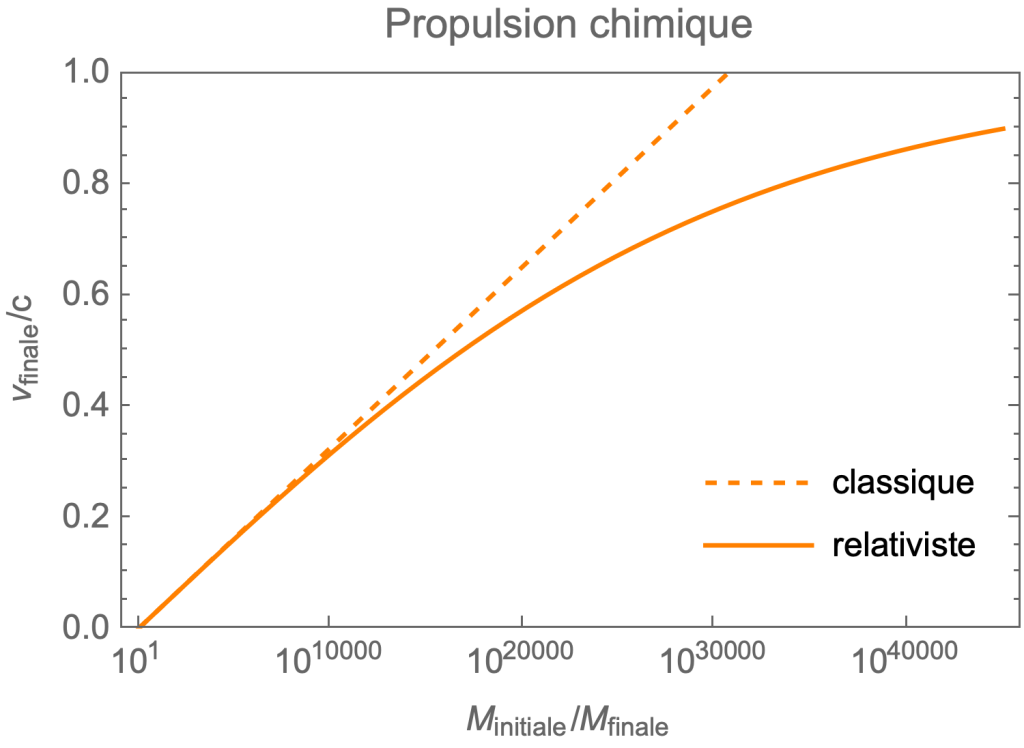
Vitesse finale de la capsule (en unités de la vitesse de la lumière) en fonction du rapport des masses entre la masse totale initiale, et la masse de la capsule. Cas d’une fusée à énergie chimique idéale.
Source : de l’auteur.

Pour atteindre une vitesse de l’ordre du tiers de celle de la lumière avec une propulsion chimique, il faudrait que la masse initiale soit 10^{10000} plus élevée que la masse initiale. 10^{10000} signifie, un 1 suivi de 10000 zéros. Ce nombre est tout simplement délirant puisque le nombre d’atomes dans l’Univers observable est de l’ordre de 10^{80}, soit un 1 avec 80 zéros. Une fusée à énergie chimique ne pourra jamais atteindre des vitesses de l’ordre d’une fraction non négligeable de celle de la lumière. Jamais. Et en prenant en compte la relativité, la situation est encore pire à mesure qu’on cherche à s’approcher de la vitesse de la lumière.

Atteindre une étoile située à quelques années-lumière prendrait des dizaines de milliers d’années avec ce système de propulsion puisqu’il faudrait se contenter d’une vitesse d’escargot. Il faut donc nécessairement utiliser des modes de propulsion utilisant beaucoup plus efficacement l’énergie du carburant. La même figure ci-après pour une fusée à énergie d’annihilation est déjà bien plus encourageante puisqu’il faut une masse initiale seulement 10 fois plus grande pour dépasser le tiers de la vitesse de la lumière.

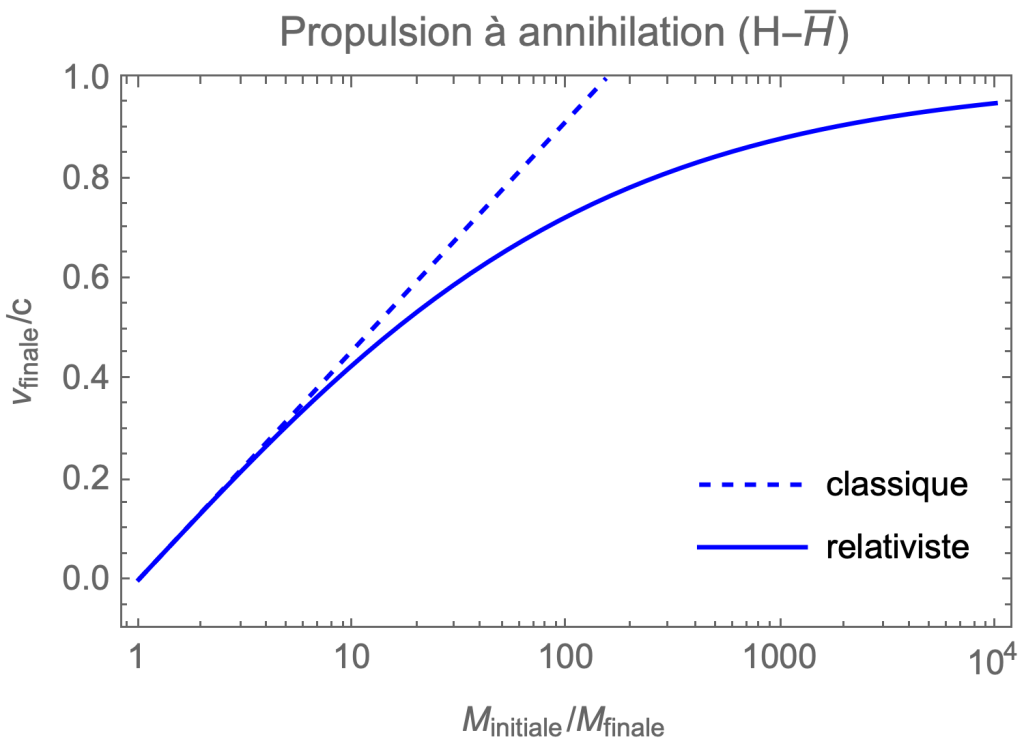
Vitesse finale de la capsule (en unités de la vitesse de la lumière) en fonction du rapport des masses entre la masse totale initiale, et la masse de la capsule. Cas d’une fusée à annihilation idéale.
Source : de l’auteur.

Cependant, si on souhaite se rapprocher grandement de la vitesse de la lumière afin de diminuer le temps de trajet, le rapport des masses s’envole. Pour atteindre 95% de la vitesse de la lumière, il faut que la masse initiale de la fusée parfaite avec le moteur de science-fiction idéal soit 10000 fois plus grande que la masse de la capsule. Comme détaillé plus bas, nous avons malheureusement de bonnes raisons de vouloir voyager à de telles vitesses.

Par ailleurs, il est crucial que ce moteur à annihilation atteigne son rendement théorique maximal. Toute dégradation de sa performance, c’est-à-dire une diminution de la vitesse d’éjection des gaz, est catastrophique à cause de ce satané logarithme. Une division par deux de la vitesse d’éjection fait passer un rapport des masses de 10 à 100, tandis qu’un rapport de 10 000 deviendra 100 000 000.

Temps de trajet

La raison principale pour vouloir atteindre une vitesse non négligeable par rapport à celle de la lumière est le temps de trajet. Comme évoqué plus haut, les trajets en fusée à énergie chimique seraient irrémédiablement trop longs à l’échelle de la vie humaine. Si on prend comme exemple concret le cas de l’étoile la plus proche, Alpha du Centaure, située à environ 4 années-lumière, une vitesse qui serait 1000 fois plus petite que celle de la lumière impliquerait un trajet de 4000 ans. Alors qu’à la moitié de la vitesse de la lumière, le trajet serait de 8 ans.

Mais 8 ans pour qui ? Pour le voyageur ? Ou pour celui qui est resté sur Terre ? Il est notoire que des jumeaux séparés par un tel voyage ne vieilliront pas de la même manière, le temps n’étant pas une grandeur absolue pour la physique relativiste. Les 8 ans seraient valables pour celui qui serait resté sur Terre. Pour celui qui voyage, le temps passé dans la capsule serait plus court. Et d’autant plus court qu’il voyagerait à une vitesse proche de celle de la lumière.

Afin de voyager à la plus grande vitesse possible, il est nécessaire d’accélérer le plus possible. Cependant, si le voyage est habité, il n’est pas raisonnable de faire subir aux passagers une accélération supérieure à quelques fois celle de la Terre. Envisager une accélération constante à 2g au lieu des 1g sur la Terre paraît déjà un choix plus qu’ambitieux. Sur le graphe suivant on peut constater l’influence que l’accélération constante aurait sur la durée du trajet.

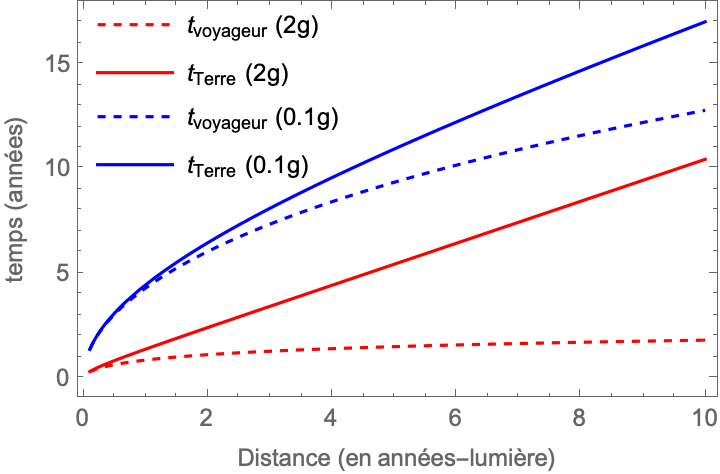
Durée du voyage (exprimée en années terrestres), en fonction de la distance du voyage. Deux accélérations sont envisagées : 2g et 0.1g. Les durées pour les personnes restées sur Terre sont en trait continu, tandis que pour les voyageurs, les durées plus courtes sont en pointillés.
Source : de l’auteur.

Bien évidemment les trajets sont plus longs avec une fusée accélérant plus faiblement. De plus lorsque l’accélération est plus importante, l’écart se creuse entre les durées sur Terre, et celles vécues par les voyageurs. Pour voyager sur une distance de 10 années-lumière, les voyageurs ayant accéléré constamment à 2g n’auraient vieilli que de deux ans, tandis que sur Terre 10 ans se seraient écoulés. Avec une accélération faible de 0.1g, ces durées seraient respectivement de 13 ans et 17 ans, et l’écart relatif serait donc moins important.

Cela s’explique par le fait que dans le premier cas, l’essentiel du voyage aurait eu lieu à des vitesses proches de celle de la lumière, une condition nécessaire pour que l’effet de contraction des durées soit perceptible. Sur le graphe suivant on peut observer la vitesse de la fusée (en unités de celle de la lumière) en fonction de l’éloignement à la Terre.

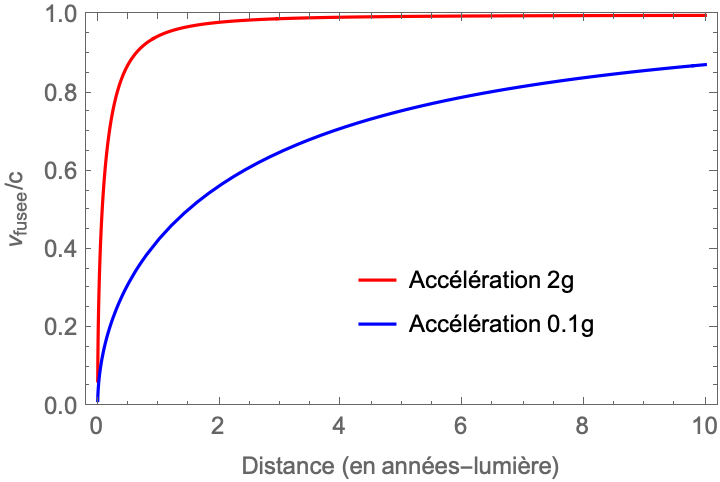
Vitesse de la fusée (en unité de celle de la lumière), en fonction de la distance parcourue. Avec une accélération de 2g, la vitesse est déjà 95% de celle de la lumière après avoir parcouru une année lumière.
Source : de l’auteur.

Quantité de carburant

Accélération constante

L’affaire est entendue, il faut une fusée parfaite, un moteur de science-fiction, et subir plusieurs années le poids d’un éléphant sur le dos. Mais même en faisant fi de tous ces aspects, est-ce pour autant réalisable physiquement ? Quel carburant doit-on embarquer pour accélérer ainsi constamment de la sorte ?

Sur le graphe suivant on peut voir quel serait le rapport des masses nécessaire pour parcourir une distance donnée en choisissant d’accélérer constamment à 2g.

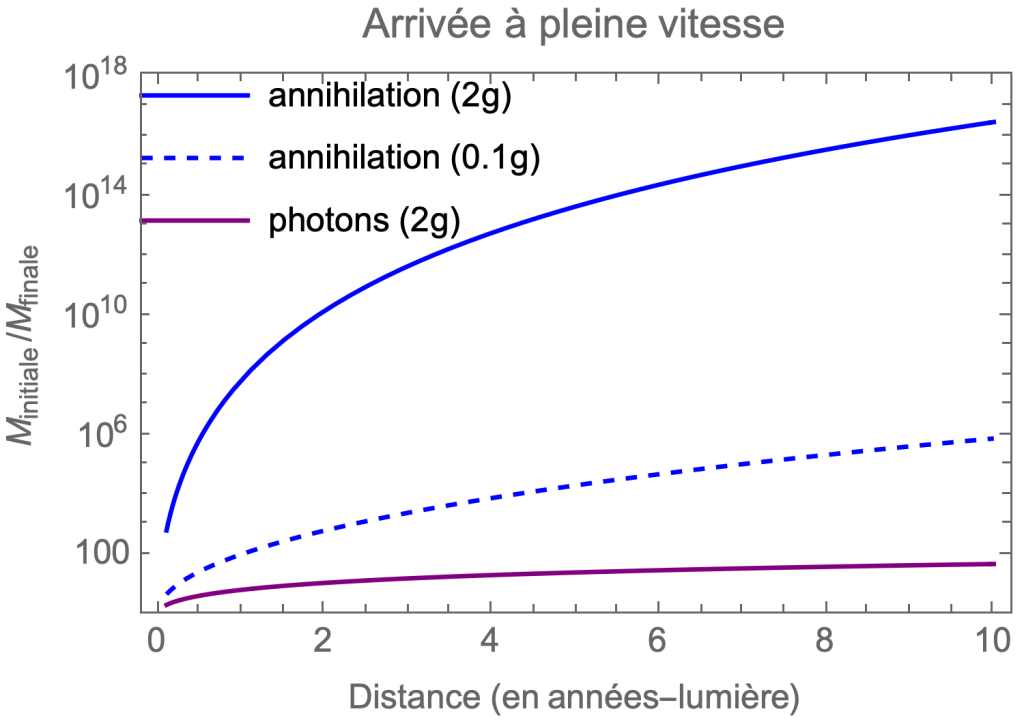
Rapport entre la masse initiale et la masse de la capsule, en fonction de la distance parcourue.
Source : de l’auteur.

Pour parcourir 1 année-lumière avec la propulsion par annihilation, il faudrait que la masse initiale soit 100 millions de fois supérieure à celle de la capsule ! En acceptant une accélération faible à 0.1g, et donc un trajet très long, la situation serait bien meilleure puisque pour 1 année-lumière il faudrait une fusée seulement 100 fois plus massive que la capsule, comme les fusées classiques actuelles. Mais il n’y a aucun système stellaire à cette distance, le plus proche étant à 4 années-lumière.

La situation empirant avec la distance, avec une accélération de 0.1g il faudrait de nouveau une fusée 1 million de fois plus massive que la capsule pour parcourir 10 années-lumière. À l’échelle de la galaxie, 10 années-lumière, c’est la banlieue du système solaire, là où on trouve nos premières étoiles voisines. Le centre de la galaxie est à environ 30 000 années-lumière et la galaxie d’Andromède à 2 000 000 d’années-lumière. Chercher à parcourir 10 années-lumière est donc pourtant plus que modeste pour un voyage interstellaire. C’est comme si en randonnée votre objectif était d’aller rencontrer votre voisin de palier.

Optimisation de l’accélération

Le problème vient avant tout du fait qu’on a considéré un trajet à accélération constante. Accélérer c’est gâcher du carburant. Mais à voyager trop lentement, les durées des trajets deviennent déraisonnables. Le bon compromis serait d’accélérer jusqu’à une vitesse non négligeable au regard de celle de la lumière, puis de couper le moteur, et de continuer le trajet à vitesse constante.

Dans le cas d’une fusée à annihilation accélérant peu, c’est-à-dire à 0.1g, la phase d’accélération pour atteindre le tiers de la vitesse de la lumière dure environ 4 ans (pour les voyageurs mais également en temps terrestre car les effets relativistes sont alors minimes) et permet d’atteindre une distance d’une année-lumière avec une fusée seulement 100 fois plus massive que la capsule. Ensuite il faut 3 ans pour parcourir chaque année-lumière puisqu’on voyage au tiers de la vitesse de la lumière. Pour être précis, c’est légèrement moins de 3 ans pour les voyageurs (environ 5% de moins) à cause des effets relativistes, soit 2.83 ans par année-lumière parcourue. Pour parcourir 10 années-lumière, il faudrait donc vieillir d’environ 4 + 9 \times 2.83 \simeq 30 ans, un voyage sans retour vraisemblablement.

On pourrait éventuellement utiliser un moteur plus efficace que le moteur à annihilation. Il faudrait alors utiliser un moteur à photons, le moteur parfait, celui qui convertirait tout le carburant en énergie. Malheureusement, on a déjà vu que c’était impossible, tout d’abord parce qu’on ne peut diriger les photons dans une même direction, et ensuite car ceux-ci détruiraient nécessairement la capsule. C’est bien dommage, car avec une masse initiale de seulement 100 fois celle de la capsule, on pourrait parcourir 10 années-lumière en accélérant constamment à 2g, et pour un temps de trajet pour les voyageurs d’un peu moins de deux ans (mais forcément supérieur à 10 ans pour ceux restés sur Terre).

Voyager c’est bien, visiter c’est mieux

Jusqu’à présent, nous avons considéré des voyages pendant lesquels on ne fait qu’accélérer, ou éventuellement des voyages lors desquels on garde une vitesse constante en coupant le moteur pour économiser le carburant au prix d’un voyage beaucoup plus long. Mais une fois arrivés au système stellaire souhaité, on ne va rien pouvoir faire si on arrive à pleine vitesse ! Il faut impérativement prévoir une phase de décélération.

Pour cela il faut accélérer pendant la première moitié du trajet, et décélérer au cours de la deuxième moitié. De même, dans la méthode consistant à couper le moteur une fois atteinte une certaine vitesse, il faut alors tout de même prévoir une phase symétrique de freinage.

Tout d’abord le freinage rallonge un peu la durée du trajet puisqu’on voyage plus lentement pendant une partie du voyage. Mais pire encore, cela augmente considérablement le rapport des masses nécessaire. On doit gâcher des ressources et perdre du temps ! Sur le graphe ci-dessous, on a tracé le rapport entre la masse initiale et la masse de la capsule pour un voyage au cours duquel on accélère pendant la première moitié du trajet, et on décélère pendant la deuxième moitié, en fonction de la distance totale du trajet.

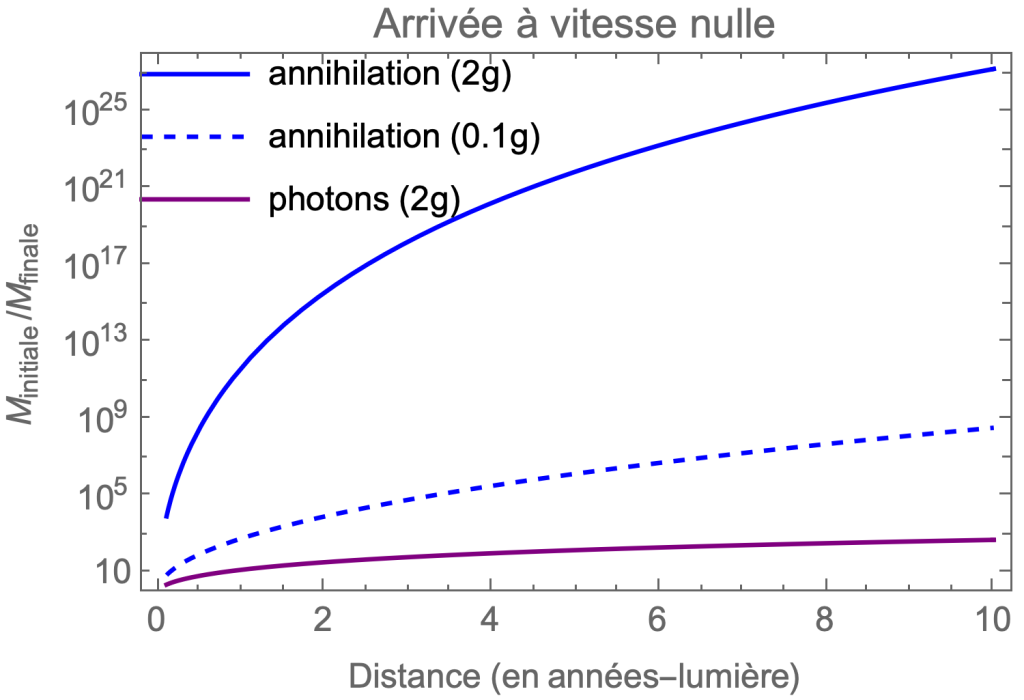
Rapport entre la masse initiale et la masse de la capsule, en fonction de la distance totale du trajet, pour une arrivée en douceur à destination.
Source : de l’auteur.

La situation devient catastrophique avec un rapport des masses qui excède 10^{27} pour parcourir 10 années-lumière en accélérant et décélérant à 2g. Si la capsule faisait 1 tonne, la fusée devrait faire la masse du soleil initialement ! Même avec une accélération plus lente à 0.1g, la fusée devrait faire plus de 100 millions de fois la masse de la capsule. C’est totalement irréaliste.

Avec la fusée à propulsion parfaite (fusée à photons), par ailleurs fondamentalement impossible à réaliser, la situation serait encore gérable puisque le rapport des masses serait de l’ordre de 1000. Mais cette fusée est impossible.

Encore une fois, il semblerait que le bon compromis reposant sur un moteur à annihilation consiste à accélérer lentement, puis couper le moteur une fois atteint le tiers de la vitesse de la lumière, et remettre le moteur vers la fin pour freiner. Il n’y a rien de gratuit, et la phase de freinage fait passer la masse de la fusée à 10 000 fois celle de la capsule, alors que comme vu précédemment il suffisait de seulement 100 fois plus lorsqu’on se contentait d’arriver à destination à pleine vitesse.

Pour réduire la masse, la seule solution c’est de moins accélérer, pour atteindre une vitesse de croisière plus faible, mais cela rallonge d’autant les trajets. Il est alors nécessaire de rallonger considérablement la vie humaine, par exemple par hibernation, ou bien d’envisager des voyages avec des équipages qui se reproduisent. On peut également explorer les systèmes stellaires par des vols inhabités, comme on l’a fait pour le système solaire, mais ces missions s’étaleraient sur des générations.

Conclusion

Il est clair que les voyages interstellaires sont (quasiment) impossibles. Non parce qu’on ne dispose pas encore de la bonne technologie, mais parce que même si l’on disposait de la technologie ultime, à savoir la propulsion par annihilation matière-antimatière dans des fusées infiniment légères, cela serait toujours insuffisant. Pour éviter une masse de fusée délirante, il faudrait réduire l’accélération et se contenter d’une vitesse de croisière bien inférieure à celle de la lumière.

Cela impliquerait alors des durées de trajets immensément élevées, en centaines ou milliers d’années pour lesquelles les effets de contraction du temps ne se font pas ressentir pour les voyageurs. Fondamentalement, la limitation est l’échelle de temps de la vie humaine, et au delà celle de la civilisation associée.

De plus, toute imperfection dans la conversion d’énergie chaufferait irrémédiablement la fusée. Les tuyères des fusées à énergie chimique doivent déjà être capables de résister à des grandes températures, alors que seulement 10^{-10} de l’énergie du carburant est convertie en énergie utile. Le problème serait immensément plus grand avec la conversion d’énergie efficace des moteurs à annihilation, car rien ne peut refroidir facilement dans le vide.

Les lois de la thermodynamiques sont parfaitement établies et incontournables, et selon Semyonov (2014) ce problème du refroidissement nécessaire à cause de l’imperfection du moteur suffirait à interdire tout rêve de fusée interstellaire rapide.

On lit souvent que le génie humain est infini et permettra de repousser toutes les limites. Cependant, ce que cet optimisme béat ignore, c’est que notre connaissance est déjà si avancée qu’elle est capable de déterminer des limites fondamentales indépassables. La structure relativiste de l’espace-temps, et la physique de particules sont aujourd’hui des connaissances scientifiques indiscutables.

Cela nous permet d’affirmer que nous ne pouvons rien voir d’autre que l’Univers observable, ce qui en soi dépasse déjà l’entendement, et qu’en pratique nous sommes confinés dans notre coin de la Voie Lactée. Lorsque nous quitterons le système solaire, cela sera pour un voyage au long cours, sans retour, une fuite en avant. On sait même que cela devra avoir lieu avant environ 4 milliards d’années, avant la fin de vie du Soleil. Nous ne serons d’ailleurs probablement même plus la même espèce, voire la même forme de vie.

Concrètement, si on raisonne à l’échelle de notre civilisation, cela implique qu’il faudra se contenter de notre système solaire. Les ressources intéressantes, c’est-à-dire tout ce qui est plus lourd que l’hydrogène ou l’hélium et qui a été fabriqué par les générations passées d’étoiles, sont situées dans les astres rocheux du système solaire.

Et ça tombe bien puisqu’environ 50.2% de cette masse rocheuse est contenue dans la Terre. Venus, la plus inhospitalière, en possède environ 41%, Mars 5.4%, Mercure 2.8%, et enfin la Lune 0.6%. La masse présente dans tous les astéroïdes est par ailleurs vraiment négligeable. En pratique, l’espèce humaine vit donc dans un monde fini bien identifié, la Terre, et il vaut mieux prendre cette donnée en compte plutôt que d’espérer naïvement que les frontières soient repoussées indéfiniment.

Pour aller plus loin

Tous les chiffres présentés ont volontairement été arrondis. On retrouvera des tableaux résumant les principales caractéristiques des voyages à accélération constante dans le cas d’un moteur parfait (\epsilon = 1) sur la page de John Baez.

Pour aller plus loin je recommande également le simulateur de David Allan Wright avec le détail des équations permettant de relier vitesse, distance et temps au cours d’un trajet à accélération constante. Une dérivation rigoureuse et moderne peut également être trouvée à la section 4.2 de l’article de U. Walter. Pour les plus impatients, je recopie les relations sans démonstration ci-dessous.

On note d la distance parcourue, t le temps écoulé sur la Terre, \tau le temps écoulé pour les voyageurs, a l’accélération de la fusée supposée constante, v_e la vitesse d’éjection des gaz. Les relations entre temps et distance sont alors

(4)   \begin{equation*}\frac{a t}{c} = \sinh\left(\frac{a \tau}{c}\right),\qquad\frac{a d}{c^2} = \cosh\left(\frac{a \tau}{c}\right)-1 = \sqrt{1+ \left(\frac{a t}{c}\right)^2} -1\,.\end{equation*}

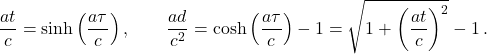
Le rapport des masses nécessaire M_{\rm initiale} / M_{\rm finale} est alors déterminé par

(5)   \begin{equation*}\ln \left(\frac{M_{\rm initiale}}{M_{\rm finale}} \right) = \frac{a \tau}{v_e} = \frac{c}{v_e} \cosh^{-1}\left(\frac{a d}{c^2} +1\right) = \frac{c}{v_e} \sinh^{-1}\left(\frac{a t}{c}\right)\,.\end{equation*}

Il faut ensuite adapter ces formules dans le cas d’une accélération suivie d’une décélération.

1Commencer une dissertation au lycée de cette manière était la garantie d’un 0/20. Aujourd’hui je peux enfin réaliser mon rêve de placer cette formule à juste titre.

2En remontant la courbe d’Aston depuis l’uranium, on voit qu’on peut récupérer environ 1 MeV par nucléon. Or les nucléons ont une masse de l’ordre de 940 MeV, si bien qu’on récupère bien de l’ordre de 1/940 \simeq 0.1\%. Pour la fusion depuis l’hydrogène on récupère environ 8 MeV par nucléon (en formant par exemple de l’hélium-4), donc on récupère une fraction de l’ordre de 8/940 \simeq 0.9\%.

3Pour plus de détails, voir après l’équation (17) de l’article de U. Walter.

4On oppose plus couramment physique classique et physique quantique, et la relativité fait alors partie de la physique classique. Ici j’entends par physique classique, la physique Newtonienne et non relativiste.

5Si la dérivation d’une telle formule remonte à Ackeret 1946, dont la lecture en Allemand m’est difficile, une dérivation très claire se trouve dans l’article de U. Walter. Il suffit de remarquer qu’il faut remplacer la vitesse v_{\rm finale} par la rapidité \phi_{\rm finale} dans l’équation (2). La rapidité est un concept physique relié à la vitesse par v_{\rm finale} = c \tanh \phi_{\rm finale} et donc \phi_{\rm finale} = \ln\sqrt{\left(\frac{1+v_{\rm finale}/c}{1-v_{\rm finale}/c}\right)}, ce qui mène alors à (3).


6En réalité, l’efficacité théorique du moteur à annihilation est supérieure à 2%, mais à cause d’imperfections inévitables dans le processus de conversion (la production de photons perdus), l’équation (1) doit être appliquée en considérant une efficacité effective de 2%, ce qui conduit à une vitesse d’éjection effective de 20% de celle de la lumière.

Si vous avez aimé ce billet, partagez-le, notamment sur les réseaux sociaux avec les boutons ci-dessous. Et pour recevoir une notification à chaque nouveau billet, vous pouvez vous abonner avec votre adresse mail sur la colonne à droite.

Suivez-moi aussi sur Twitter : @CyrilPitrou

Image Pixabay.

CatégorieEnergie
Mots-clésénergie nucléaire ressources spatiales