Quelle intermittence pour l’énergie solaire ?

Les panneaux solaires ne fonctionnent que quand le soleil brille. Derrière cette évidence, quelle est la variabilité de l’énergie solaire ? Comment peut-on optimiser le placement des panneaux solaires ?

Trajectoire apparente du soleil

Les saisons

Pour répondre à cette question, il faut d’abord savoir quelle est la trajectoire apparente du soleil dans le ciel en chaque point de la Terre. Il s’agit d’une ellipse, c’est-à-dire d’un cercle légèrement allongé. En exagérant cela ressemble à la figure suivante :

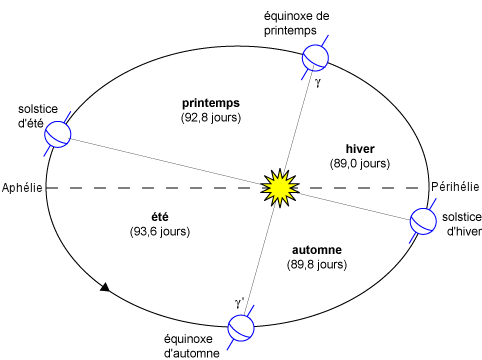
On peut assez facilement obtenir des expressions utiles si on suppose que la Terre tourne autour du soleil sur un cercle. L’ellipticité de l’orbite terrestre étant assez faible (de l’ordre du pourcent), la négliger ne va introduire que des erreurs de l’ordre du pourcent. Dans ce cas là, toutes les saisons durent exactement un quart d’année, soit 91.31 jours (un quart d’année sidérale). On rappelle que les saisons sont précisément dues au fait que l’axe de rotation de la Terre n’est pas exactement perpendiculaire au plan dans lequel évolue la Terre (le plan de l’écliptique) et n’ont rien à voir avec la distance entre la Terre et le Soleil.

Sur le schéma précédent, on constate qu’à cause de cette inclinaison de l’axe de rotation de la Terre de 23.45 degrés, la direction Terre-Soleil n’est en général pas dans le plan de l’équateur, sauf aux équinoxes. Dit différemment, parfois c’est le pôle nord qui pointe un peu plus vers le soleil (et c’est l’été dans l’hémisphère nord, au sens de la période printemps-été), parfois c’est le pôle sud qui pointe vers le soleil (et c’est l’hiver dans l’hémisphère nord, au sens de la période automne-hiver). Le passage d’une époque à l’autre se fait lors des équinoxes. A ces moments précis, l’axe de rotation de la Terre y est bien sûr toujours incliné, mais pas vers le soleil si bien que la direction du soleil vu depuis la Terre est alors exactement dans le plan de l’équateur terrestre.

La déclinaison du soleil

Vu de la Terre, on caractérise le fait que la direction du soleil n’est pas dans le plan de l’équateur terrestre en utilisant un angle appelé déclinaison. Quand l’angle de déclinaison est positif, le soleil est au dessus de l’équateur (signifiant que le pôle nord est partiellement dirigé vers le soleil) et c’est l’été dans l’hémisphère nord, ce qui correspond à la partie gauche de la figure 1. Inversement lorsque la déclinaison est négative, le soleil est plutôt en dessous de l’équateur (le pôle sud est partiellement dirigé vers le soleil), et c’est l’été dans l’hémisphère sud, ce qui correspond à la partie droite de la figure 1. Sur la figure 2, on a tracé cet angle de déclinaison en prenant comme jour de référence non pas le premier janvier, mais l’équinoxe d’été (en général le 21 juin). On retrouve qualitativement la variation de la déclinaison simplement en examinant dans la figure 1 quel pôle pointe vers le soleil.

Les angles du soleil

La position du soleil dans le ciel en un point du globe terrestre est décrite par deux angles. Tout d’abord la hauteur est l’angle entre l’horizon et le soleil, et caractérise l’ensoleillement. On l’appelle aussi angle d’élévation du soleil. Quand celui-ci est nul, le soleil se lève ou se couche, et quand celui-ci vaut 90 degrés, le soleil est parfaitement au zénith et le flux solaire reçu au sol est maximal. Il est aussi souvent très pratique de considérer l’angle entre le soleil et le zénith directement, appelé angle zénithal et noté . Celui-ci vaut 0 degré quand le soleil est au zénith, et 90 degrés au lever ou au coucher du soleil.

Ensuite le deuxième angle qui caractérise la positon du soleil est l’azimuth ou l’angle azimuthal, défini comme la direction de la projection sur l’horizon, mesurée par rapport à la direction du sud. Cet angle est noté . Ces deux angles sont représentés sur la figure ci-dessous :

Une fois que l’on a supposé que la Terre tourne autour du soleil sur un cercle, il est facile de déterminer ces angles, et donc la position du soleil, en fonction du jour et de l’heure, mais cela nécessite tout de même d’être assez à l’aise avec la géométrie. J’ai donc réuni les expressions nécessaires permettant de déterminer la trajectoire du soleil dans un formulaire. Si vous êtes allergique aux équations, surtout ne l’ouvrez jamais car vous risqueriez une syncope. Ici, on ne va s’intéresser qu’à l’application au problème des panneaux solaires et pour cela nous aurons uniquement besoin des courbes obtenues à partir de ces formules barbares. Les allergiques à la trigonométrie, vous pouvez donc continuer de lire ce billet sans risque pour votre santé.

Toutes les courbes donnant la trajectoire du soleil vont dépendre de la latitude du point considéré sur la Terre. Pour l’équateur la latitude vaut 0 degré, puis elle augmente dans l’hémisphère nord pour atteindre 90 degrés au pôle nord. Inversement la latitude diminue dans l’hémisphère sud pour atteindre -90 degrés au pôle sud.

L’ensoleillement sur le globe

On représente la position du soleil dans un diagramme avec en abscisse l’azimuth du soleil, et en ordonnée l’angle au dessus de l’horizon. Dans la figure ci-dessous, on retrouve les trajectoires pour un point sur l’équateur (latitude 0 degré), un point quasiment au niveau du tropique (latitude 20 degrés), un point en zone tempérée (latitude 40 degrés) et un point assez au nord mais néanmoins en dessous du cercle polaire pour éviter les problèmes de soleil qui ne se couche pas (latitude 60 degrés). Par ailleurs, dans toutes les figures qui suivent on adopte le code couleur suivant : les courbes rouges correspondent au solstice d’été, et les courbes bleues correspondent au solstice d’hiver. Enfin les courbes violettes correspondent aux équinoxes (un mélange de rouge et bleu !) .

Pour les latitudes non comprises dans la zone intertropicale (les deux graphes du bas), on voit bien que le soleil se lève quelque part vers l’est puis monte dans le ciel et passe par une hauteur maximum lorsque son azimuth est plein sud, puis redescend pour se coucher quelque part vers l’est. Au solstice d’été le soleil se lève en fait au nord-est (l’azimuth du lever est plus petit que -90 degrés) et se couche ou nord-ouest (l’azimuth du coucher est plus grand que +90 degrés), tandis qu’au solstice d’hiver il se lève au sud-est, fait une petite course dans le ciel pas très haut, et se recouche rapidement au sud-ouest. Entre les deux, aux équinoxes, le soleil se lève exactement à l’est (azimuth de -90 degrés au lever) et se couche exactement à l’ouest (azimuth de +90 degrés au coucher), et la journée dure précisément 12 heures. Cette propriété des équinoxes –qui se retrouve dans l’étymologie même du mot– est d’ailleurs valable pour toutes les latitudes si on regarde les différents graphes, car lors des équinoxes la déclinaison est nulle, et dans ce cas là tout est très simple.

Dans la zone intertropicale, la lecture de la trajectoire du soleil est moins évidente. Prenons le cas de l’équateur (latitude 0, donc le graphe en haut à gauche). Au solstice d’été le soleil va se lever vers l’est (azimuth négatif), puis passer par le nord à midi. Comme l’azimuth est défini par rapport au sud, celui-ci diminue au cours de la matinée, jusqu’à la valeur -180 degrés à midi exactement lorsque le soleil est au nord. Puis sa valeur se transforme en +180 degrés pour rediminuer l’après-midi lorsque le soleil redescend pour se coucher à l’ouest. Lors de l’équinoxe au niveau de l’équateur (points violets en haut à gauche), on voit même que le soleil reste exactement à l’est toute la matinée (azimuth -90 degrés) en montant dans le ciel, jusqu’à passer au zénith et redescend exactement à l’ouest (azimuth +90 degrés) tout l’après-midi. En revanche en hiver pour un point de l’équateur, le soleil passe toujours par le sud et on retrouve une forme simple de la trajectoire.

En général, le soleil ne peut culminer au zénith que dans la zone intertropicale, et seulement à certaines dates. On peut montrer que c’est le cas les jours où la déclinaison est égale à la latitude du lieu considéré. Par conséquent, en portant en ordonnée la latitude dans la figure 2, on peut lire sur l’abscisse les deux jours lors desquels le soleil passera par le zénith à midi. Dans les cas d’un point situé sur le tropique nord, il n’y a en revanche qu’un seul jour, à savoir le solstice d’été, et inversement pour un point situé sur le tropique sud, cela n’arrive que lors du solstice d’hiver.

Efficacité des panneaux solaires

Les courbes de la figure 4 sont intéressantes pour avoir une idée de l’ensoleillement en fonction de la position sur la Terre et le jour de l’année. Mais ce qui nous intéresse plus précisément est l’efficacité géométrique des panneaux solaires. Nous voulons savoir à quel point le soleil sera en face des panneaux. Bien sûr il faudra ensuite prendre en compte l’efficacité intrinsèque des panneaux solaires, c’est-à-dire le rendement pour convertir le flux solaire en puissance électrique, mais celui-ci ne va pas dépendre de la position du soleil. A chaque fois qu’on parlera d’efficacité des panneaux solaires dans ce billet, on parlera uniquement des effets de projection des rayons du soleil sur les panneaux solaires.

Panneaux à plat

Si on considère des panneaux disposés sur le sol horizontalement, le facteur d’efficacité est donné par , c’est-à-dire la projection de la direction du soleil avec la direction du zénith. D’une certaine manière il s’agit de l’efficacité géométrique pour un usage agricole de l’énergie solaire. Les efficacités sont tracées dans les graphiques ci-dessous.

Pour le graphe en haut à gauche correspondant à un point sur l’équateur, les courbes des solstices (rouge et bleue) sont confondues. Puis plus on monte en latitude, et plus l’efficacité et la durée du jour sont réduites en hiver. Par ailleurs la ligne noire horizontale dans chaque graphe représente la moyenne annuelle. Le soleil étant assez bas sur l’horizon pour les hautes latitudes, cette moyenne est d’autant plus réduite. On voit également que pour un point sur l’équateur pour lequel le soleil est souvent proche du zénith, la moyenne de l’efficacité est de l’ordre de 30% de l’efficacité maximale ayant lieu aux équinoxes à midi.

Panneaux mobiles

Cette manière d’installer les panneaux solaires n’est pas forcément idiote dans la zone intertropicale, mais cela devient franchement inefficace pour des latitudes plus élevées. On devrait pouvoir incliner les panneaux solaires pour les mettre le plus possible en face du soleil. Si on peut les orienter à notre guise, il est évident que le plus intéressant est de les faire toujours pointer vers le soleil. Ainsi ils produisent toujours au maximum, sauf quand il fait nuit. En moyenne annuelle la production sera donc la moitié du maximum puisqu’il fait jour la moitié du temps !

Cependant si cela est le cas pour un panneau solaire isolé, cela ne va pas forcément être le cas pour un ensemble de panneaux déployés les uns à côtés des autres. En effet lorsque les panneaux sont inclinés, ils vont éventuellement faire de l’ombre à leurs voisins. Dans le cas extrême où le soleil est juste au dessus de l’horizon, le premier panneau va faire de l’ombre à tous ceux qui sont derrière. L’efficacité géométrique d’un parc solaire va donc dépendre du taux d’occupation des panneaux solaires (la lettre comme coverage rate en anglais). Il s’agit du rapport entre la surface totale des panneaux et la surface de terrain totale sur lequel ils sont installés. De manière équivalente c’est le rapport entre la surface d’un panneau et la surface disponible au sol par panneau, donc . Si l’ombre portée par un panneau est plus grande que sa surface disponible au sol , cela signifie qu’il n’existe pas de moyen de les disposer pour qu’aucun ne fasse de l’ombre aux autres. On aura beau incliner les panneaux au fur et à mesure que le soleil descend sur l’horizon le soir, l’efficacité du parc sera alors la même qu’un terrain entièrement recouvert de panneaux solaires horizontaux, car tous les rayons du soleil incidents sur le terrain du parc solaire seront interceptés.

L’efficacité géométrique dans le cas de panneaux totalement orientables est tracée sur la figure ci-dessous. En trait continu, il s’agit de l’efficacité dans le cas où le taux d’occupation est très faible et en tirets le cas où le taux d’occupation est (soit 50%) induisant ces problèmes d’ombres. Les traits horizontaux correspondent aux moyennes annuelles. On voit que tôt le matin et tard le soir, le soleil étant bas sur l’horizon, les effets d’ombre réduisent l’efficacité des panneaux solaires. Pour les grandes latitudes, c’est particulièrement important comme réduction en hiver puisque le soleil passe la majeure partie de la journée (déjà réduite) pas très haut au dessus de l’horizon.

Lorsque l’on calcule le potentiel solaire d’une zone donnée, il faut donc bien prendre en compte le fait que l’on ne peut pas resserrer trop les panneaux, au risque de gâcher la production hivernale, celle qui est justement la plus faible. A trop vouloir serrer les panneaux on perd considérablement en efficacité.

Inclinaison vers le sud

De tels dispositifs d’inclinaison des panneaux solaires peuvent être complexes à réaliser et on pourrait préférer un dispositif simplifié où les panneaux ne peuvent que s’incliner vers le sud ou le nord en tournant autour d’un axe est-ouest. On peut déterminer pour chaque position du soleil l’inclinaison optimale vers le sud, et cela est donné par la formule (je craque et je mets quand même cette magnifique formule de trigo…)

   

Au passage, le soleil étant au sud à midi, l’azimuth y est nul et donc , si bien que l’angle d’inclinaison optimal est égal à l’inclinaison du soleil, soit . Bien évidemment, à midi il suffit d’incliner le panneau vers le sud en direction du soleil pour maximiser son efficacité, et on est rassuré de retrouver ce résultat évident. Avec ce dispositif d’inclinaison, les efficacités sont tracées dans la figure suivante. En trait continu on a considéré le cas où les panneaux sont très espacés et ne se font jamais d’ombre, et en pointillé un taux d’occupation de 0.5 avec une réduction de l’efficacité due aux problèmes d’ombre. Les traits horizontaux représentent les moyennes annuelles.

Grâce à ce dispositif simplifié, on ne fait bien évidemment pas aussi bien que lorsque l’on peut orienter parfaitement les panneaux vers le soleil, mais on fait déjà beaucoup mieux que lorsque les panneaux sont disposés à plat. A midi, comme on peut toujours orienter le panneau vers le soleil, on a une efficacité maximale pour toutes les latitudes à toutes les époques de l’année. En hiver (courbes bleues) on ne fait pas beaucoup moins bien qu’en été quand il y a du soleil, mais on produit moins tout simplement parce que les journées sont plus courtes. Mais dans tous les cas la production ne chute pas à zéro quand le soleil est rasant car l’inclinaison des panneaux permet de les placer partiellement en face du soleil.

En revanche si les panneaux ne sont pas assez espacés (courbes en pointillés), l’efficacité est d’autant plus réduite à cause des problèmes d’ombre, et cela affecte d’autant plus l’hiver où le soleil est bas sur l’horizon. Pour des hautes latitudes (graphe en bas à droite), le problème peut être très important car cela supprime quasiment toute la production en hiver (la courbe bleue en pointillée est très inférieure à la courbe bleue continue).

En été (courbe rouge), on remarque une remontée de l’efficacité tôt le matin et tard le soir. Comme le soleil se lève au nord-est et se couche au nord-ouest (dans l’hémisphère nord), on optimise la production en inclinant les panneaux vers le nord. D’ailleurs cela se voit sur la figure ci-dessous où l’on a tracé les angles d’inclinaison optimaux. On vérifie bien que les angles sont négatifs (inclinaison vers le nord), tôt et tard en été.

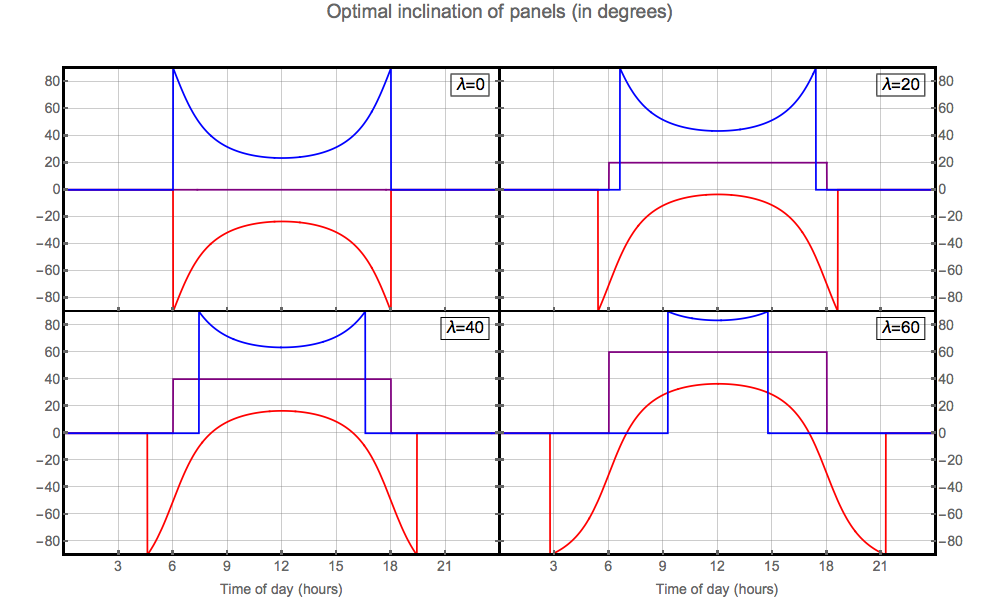
On voit également que lors des équinoxes, il suffit de maintenir un inclinaison constante (égale à l’angle de la latitude) au cours de la journée.

Inclinaison constante

Si on veut encore simplifier le dispositif, on peut considérer que les panneaux peuvent être inclinés à l’installation mais que cette inclinaison est fixe. On peut alors se poser la question de l’inclinaison optimale. On a vu que lors des équinoxes, l’inclinaison optimale est constante au cours de la journée, et égale à la latitude du lieu. L’inclinaison constante optimale va donc très logiquement être proche de cette valeur, puisqu’en été le soleil est plus haut et en hiver plus bas. Dans le graphe suivant, on a tracé en trait continu l’inclinaison optimale en fonction de la latitude. Le trait en pointillés correspond à la courbe où l’inclinaison est choisie égale à la latitude.

En pratique l’angle optimal est proche de la latitude du point considéré, mais légèrement inférieur puisque la courbe continue est légèrement en dessous de la courbe en pointillés. C’est assez logique puisque le soleil est un peu plus haut en été et un peu plus bas en hiver. Or comme les jours sont plus longs en été, mieux vaut incliner un peu moins pour optimiser plus les jours d’été que les jours d’hiver.

En utilisant cette inclinaison constante optimale on a tracé ci-dessous les courbes d’efficacité, avec les mêmes conventions que pour les graphes précédents.

On retrouve toujours le fait que les courbes en pointillés (le cas où le taux de couverture est de 0.5 avec des problèmes d’ombre) sont très inférieures en hiver, ce qui a tendance à baisser les moyennes annuelles pour les grandes latitudes.

Caractériser la variabilité

En ayant passé en revue les facteurs géométriques affectant l’efficacité des panneaux solaires pour différent dispositifs, on souhaite maintenant caractériser l’irrégularité de la production. D’un point de vue pratique, ce qui nous intéresse c’est de savoir à quel point les fortes productions sont plus élevées que la moyenne, car c’est ce qui va déterminer le surdimensionnement du réseau électrique nécessaire pour absorber la production des pics, en admettant que l’on dispose d’un moyen de stocker toute cette énergie (ce qui par ailleurs est très loin d’être le cas). De manière équivalente on peut regarder le rapport entre la moyenne de la production et les pics. C’est alors exactement similaire au facteur de charge d’un moyen de production, donné par le rapport entre la puissance moyenne et la puissance installée, cette dernière ne pouvant être fournie que lors des pics. Plus ce rapport est faible, et plus il faut surdimensionner le réseau électrique, par rapport à un réseau conçu pour ne transporter que la puissance moyenne ou légèrement plus.

Voici un tableau récapitulatif des rapports moyenne/pic (noté ) pour les différents systèmes d’installation décrits précédemment.

	lat = 0	lat = 10	lat = 20	lat = 30	lat = 40	lat = 50	lat = 60
Horizontal	0.333	0.310	0.289	0.270	0.252	0.233	0.216
Inclinaison constante, couverture=0	0.305	0.305	0.305	0.303	0.301	0.297	0.288
Inclinaison constante, couverture = 0.5	0.305	0.305	0.304	0.301	0.293	0.266	0.230
Inclinaison variable, couverture=0	0.344	0.344	0.344	0.344	0.344	0.344	0.344
Inclinaison variable, couverture = 0.5	0.337	0.336	0.335	0.331	0.318	0.290	0.254
Vers le soleil, couverture=0	0.5	0.5	0.5	0.5	0.5	0.5	0.5
Vers le soleil, couverture=0.5	0.415	0.413	0.408	0.399	0.379	0.345	0.304

Tout d’abord, le seul cas où ce rapport est honorable, c’est à dire , correspond au cas où on peut parfaitement orienter les panneaux vers le soleil. Il faut donc prévoir un dispositif motorisé ou un système de vérins pour ajuster en permanence cette orientation. Mais ce cas correspond également à un parc où les panneaux sont très espacés et ne peuvent se faire de l’ombre. Si on choisit un taux d’occupation de comme c’est le cas dans les projets développés hors désert, on est plutôt autour de en zone tempérée.

Si on examine ensuite le dispositif le plus simple avec une inclinaison constante, on obtient un facteur de charge autour de en zone tempérée. Cependant, cela nécessite des panneaux assez espacés. Si on les place avec un taux d’occupation de , l’efficacité se réduit autour de en zone tempérée.

Autrement dit, avec des dispositifs sophistiqués, placés assez proches les uns des autres pour éviter la concurrence des sols avec d’autre usages (l’agriculture notamment), il faut surdimensionner le réseau d’un facteur 2.85. Mais si on se contente de panneaux inclinés de manière constante, il faut surdimensionner au moins d’un facteur 3.6.

Irradiation solaire

Cependant toute cette étude n’a pas pris en compte deux facteurs limitants. Tout d’abord lorsque le soleil est juste au dessus de l’horizon, l’atmosphère absorbe une grande partie du rayonnement solaire. Il s’agit de la diffusion qui disperse plutôt le bleu et donc ne reste dans le flux solaire que le rouge, ce qui fait de magnifiques levers et couchers du soleil. Une bonne manière de se rendre compte de la perte de flux solaire, est de se souvenir qu’il est inconscient de regarder le soleil de face la journée, au risque de devenir aveugle, tandis qu’on peut regarder le lever et le coucher du soleil sans trop de risques. En pratique, tous les calculs d’efficacité doivent prendre en compte cette atténuation lorsque le soleil est bas sur l’horizon, et cela va réduire de manière non négligeable la production en hiver où le soleil passe une grande partie de son temps très bas sur l’horizon.

Ensuite, nous avons considéré un cas théorique sans nuages. Mais malheureusement il n’y a pas tous les jours un soleil éclatant… La moyenne en France est de 2054 heures de soleil sur les 4383 heures de la durée cumulée des jours d’une année, soit environ 47% du jour. Même sur la Côte d’Azur, il n’y a que 2447 heures d’ensoleillement soit environ 56% du jour.

Bien sûr les panneaux solaires produisent aussi par temps nuageux, même si la réduction de leur production est conséquente. A cause de cette production faible mais non nulle, il est plus pertinent de caractériser la réduction du flux solaire non pas en comptant le nombre d’heures d’ensoleillement, mais en regardant la réduction du flux solaire moyen par rapport au flux théorique maximal.

Comme nous avons déterminé la position du soleil dans le ciel en tout point du globe, il est facile de prendre la moyenne de la puissance solaire reçue par unité de surface si on néglige l’effet des nuages. Il s’agit tout simplement de la moyenne de –que d’ailleurs nous avons déjà tracée sur la figure 5 en traits horizontaux– multipliée par le flux solaire moyen au dessus de l’atmosphère. J’appelle cette quantité l’irradiation solaire moyenne maximale, et elle est tracée en fonction de la latitude sur la figure suivante :

On remarque que cette irradiation solaire moyenne maximale n’est pas nulle aux pôles, et ce grâce à l’inclinaison des pôles, faisant qu’il existe une saison avec de la lumière en continu, et une saison dans le noir. Par ailleurs, la moyenne de l’irradiation solaire maximale sur le globe –soit 340.25W/m² ou 2983 kWh/m²/an– est égale au quart du flux solaire au dessus de l’atmosphère, soit 1.361 kW/m² ou 11 930 kWh/m²/an. Ce facteur vient du fait que la Terre reçoit le flux du soleil sur un disque de surface (où est le rayon de la Terre), mais sa surface est . Au passage, cette division par 4 dans le contexte de l’équilibre radiatif de la Terre, aussi simple qu’elle soit à comprendre, a permis à un climatosceptique Français (et membre de l’Académie des Sciences) assez célèbre de se planter en beauté. Vous en savez déjà plus que lui maintenant, alors continuez à lire Le Dernier Carbone !

On peut maintenant comparer l’irradiation solaire maximale avec celle mesurée en différents points du globe sur la carte suivante :

On constate que dans le Sahara (latitude d’environ 15 degrés) l’irradiation moyenne maximale est environ de 2600 kWh/m²/an alors que le maximum théorique lu depuis la figure 11 est autour de 3500 kWh/m²/an. Le rapport des deux (environs 0.75) indique les pertes liées notamment aux nuages à cet endroit. Dans le nord de la France à une latitude de 50 degrés, on mesure environ 1000 kWh/m²/an alors que le maximum théorique est autour de 2500 kWh/m²/an. Le rapport est d’environ 0.40, et donc bien plus faible ! On constate clairement sur cette carte que l’irradiation dépend du climat local. Ainsi même si le maximum théorique est au plus haut à l’équateur (voir figure 11), ce n’est pas là que l’irradiation effective est la plus haute puisqu’il s’agit de zones très humides et nuageuses, et non de déserts.

Conclusion

Au final, en prenant en compte la réduction d’irradiation solaire, on constate qu’il est parfaitement justifié de diviser les efficacités de la table ci-dessus par un facteur 2 au minimum. Au doigt mouillé, il faudrait surdimensionner le réseau d’un facteur 7 car le facteur de charge typique d’un parc solaire serait alors plutôt autour de . Cela est d’ailleurs ce qui est généralement constaté pour la production d’électricité solaire dont le facteur de charge est compris entre 11% et 15%. Et si on choisissait d’écrêter la production en jetant la production trop abondante lors des pics, on ne ferait que diminuer le taux de retour énergétique des panneaux solaires. Sur ces sujets je vous encourage à regarder la vidéo du Réveilleur.

Pourrait-on plutôt aller chercher l’énergie solaire dans le désert ? En effet, l’efficacité géométrique pour les basses latitudes est plutôt autour de et même plus si on espace beaucoup les panneaux, le soleil passe peu de temps juste au dessus de l’horizon, la différence été/hiver est peu marquée, et les nuages y sont peu fréquents. D’apparence une bonne solution pour la production d’énergie solaire, cela présente d’autres problèmes que je détaillerai dans un billet à venir.

Pour aller plus loin sur les maths derrière les courbes d’efficacité, n’hésitez pas à lire les notes associées.

Si vous avez aimé ce billet, partagez-le, notamment sur les réseaux sociaux avec les boutons ci-dessous. Et pour recevoir une notification à chaque nouveau billet, vous pouvez vous abonner avec votre adresse mail sur la colonne à droite.

Suivez-moi aussi sur Twitter : @CyrilPitrou

Merci !

Image par Robert Jones de Pixabay