
Peut-on améliorer les éoliennes ?
Quelle est le rendement d’une éolienne pour produire de l’électricité à partir du vent ? Quelle est la production d’énergie éolienne typique sur terre et offshore ?
La puissance du vent
Un dispositif qui capte l’énergie du vent doit être capable d’extraire l’énergie cinétique (l’énergie liée à la vitesse du vent). Il doit donc être capable de freiner le vent et de convertir l’énergie ainsi récupérée en énergie électrique.
Intéressons-nous à une surface perpendiculaire au sens du vent. Toute l’énergie du vent récupérable pour cette surface dans un temps donné, correspond à l’énergie cinétique de l’air qui aura traversé cette surface. On comprend déjà qu’il y a peu d’intérêt à considérer une surface qui ne serait pas perpendiculaire au sens du vent, si on veut qu’un maximum d’air la traverse. L’expression de l’énergie cinétique est bien connue, et est donnée par la célèbre formule
![]()
où ![]() est la masse et
est la masse et ![]() la vitesse. L’énergie cinétique récupérable sera donc proportionnelle à la quantité de masse d’air qui traverse la surface pendant le temps considéré. La quantité de masse qui traverse par unité de temps est le débit et il est proportionnel à la densité de l’air
la vitesse. L’énergie cinétique récupérable sera donc proportionnelle à la quantité de masse d’air qui traverse la surface pendant le temps considéré. La quantité de masse qui traverse par unité de temps est le débit et il est proportionnel à la densité de l’air ![]() (plus l’air est lourd, plus il transporte de masse), à la vitesse (plus l’air va vite et plus il y a d’air qui a le temps de traverser la surface), et à la surface
(plus l’air est lourd, plus il transporte de masse), à la vitesse (plus l’air va vite et plus il y a d’air qui a le temps de traverser la surface), et à la surface ![]() (plus la surface est grande et plus il y a d’air qui la traverse). Le débit est donc donné par
(plus la surface est grande et plus il y a d’air qui la traverse). Le débit est donc donné par ![]() . On trouve alors que la puissance récupérable pour cette surface est
. On trouve alors que la puissance récupérable pour cette surface est
(1) ![]()
En pratique on préfère diviser cette expression par ![]() pour parler de puissance récupérable par unité de surface perpendiculaire au vent. On parle alors de puissance par unité de surface (dont l’unité est le W/m2, i.e. le Watt par mètre carré). En remplaçant le débit par son expression ci-dessus, on trouve que cette puissance du vent par unité de surface est
pour parler de puissance récupérable par unité de surface perpendiculaire au vent. On parle alors de puissance par unité de surface (dont l’unité est le W/m2, i.e. le Watt par mètre carré). En remplaçant le débit par son expression ci-dessus, on trouve que cette puissance du vent par unité de surface est
![]()
En unités du système international, la densité de l’air est d’environ ![]() . Cela signifie que si on exprime la vitesse du vent en mètres par seconde (10m/s, c’est 36 km/h, soit un sprinter de classe mondiale sur le 100m), alors on obtient la formule bien pratique
. Cela signifie que si on exprime la vitesse du vent en mètres par seconde (10m/s, c’est 36 km/h, soit un sprinter de classe mondiale sur le 100m), alors on obtient la formule bien pratique
(2) ![]()
A 10m/s on a un bon vent bien pénible pour les coiffures, et en application de cette formule, une puissance surfacique de 600W/m2. Et comme la puissance va comme le cube de la vitesse, si on considère une vitesse de vent deux fois plus faible, la puissance est divisée par 8 et inférieure à 100W/m2. Pour faire simple, les zones les mieux exposées en France sont au bord de mer ou dans le quart nord-ouest, comme on peut le constater sur la carte suivante :

Dans une zone ventée où la moyenne de la puissance du vent est de 500W/m2, et si on imagine pouvoir récupérer toute l’énergie du vent, alors il faut une surface de 10 000m2 (un rotor de 115m de diamètre par exemple), pour pouvoir obtenir une production de 5MW.
Au niveau Européen, on constate que le potentiel se situe essentiellement autour de la Baltique, de la mer du Nord et dans les îles britanniques :
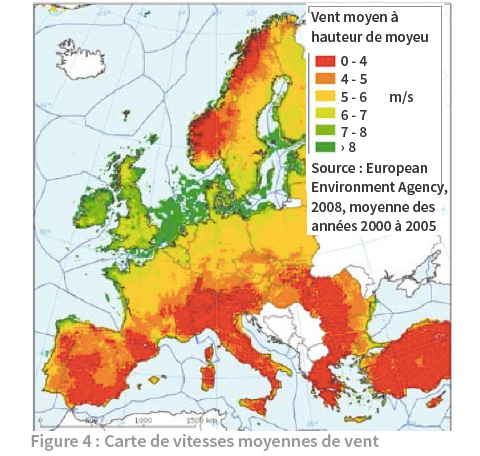
On note que cette carte n’est pas vraiment d’accord avec la précédente en ce qui concerne la zone proche de la Méditerranée en France. Mais la question essentielle qui vient immédiatement est celle de savoir quelle est la fraction que l’on peut récupérer de toute cette énergie disponible. En effet comme on va le voir, il est impossible de récupérer toute l’énergie du vent.
Rendement théorique d’une éolienne
Pour cela, il faut revenir au fonctionnement d’une éolienne. Schématiquement, la surface que ce dispositif va utiliser pour capter l’énergie du vent est celle balayée par le rotor (les pales). Pour bien comprendre ce qui arrive à l’air, on trace le tube englobant les trajectoires des particules d’air qui traversent la surface du rotor. Comme celui-ci a pour fonction de ralentir l’air la vitesse loin après la traversée de l’éolienne, notée ![]() , est inférieure à celle longtemps avant la traversée notée
, est inférieure à celle longtemps avant la traversée notée ![]() . Or comme le débit doit être constant, la surface du tube ne fait que s’agrandir. Comme un fleuve qui s’élargit voit la vitesse de l’eau qui s’y écoule fortement diminuer, le ralentissement de l’air s’accompagne d’un élargissement du lit de l’air.
. Or comme le débit doit être constant, la surface du tube ne fait que s’agrandir. Comme un fleuve qui s’élargit voit la vitesse de l’eau qui s’y écoule fortement diminuer, le ralentissement de l’air s’accompagne d’un élargissement du lit de l’air.

On peut montrer que la vitesse au niveau de l’éolienne est à mi-chemin entre celle après et celle avant, c’est-à-dire est donnée par la moyenne entre la vitesse avant et la vitesse après. Sur le schéma ci-dessus on a donc ![]() .
.
On pourrait croire qu’une éolienne qui fonctionne au mieux est une éolienne capable d’arrêter totalement l’air de sorte que ![]() , afin d’en extraire toute l’énergie cinétique. Mais à trop ralentir l’air on extrait certes très efficacement son énergie, mais on l’empêche également de passer dans le dispositif. Pour savoir ce que l’éolienne récupère vraiment il faut faire la différence entre le débit d’énergie entrante et le débit d’énergie sortante :
, afin d’en extraire toute l’énergie cinétique. Mais à trop ralentir l’air on extrait certes très efficacement son énergie, mais on l’empêche également de passer dans le dispositif. Pour savoir ce que l’éolienne récupère vraiment il faut faire la différence entre le débit d’énergie entrante et le débit d’énergie sortante :
![]()
Dans la première étape on a juste écrit la différence entre la puissance de l’air qui rentre et celle de l’air qui sort, puis pour la deuxième étape on a remplacé le débit par son expression en fonction de la vitesse de l’air au niveau de l’éolienne, en prenant en compte ![]() . On retrouve clairement le dilemme de l’éolienne dans les deux dernières parenthèses. Dans l’avant dernière on voit qu’on aurait intérêt à avoir
. On retrouve clairement le dilemme de l’éolienne dans les deux dernières parenthèses. Dans l’avant dernière on voit qu’on aurait intérêt à avoir ![]() et donc à stopper l’air totalement, mais alors on fait diminuer la dernière parenthèse liée au débit passant dans l’éolienne. Un calcul d’optimisation (pour les aficionados, une simple calcul d’extremum en dérivant par rapport à
et donc à stopper l’air totalement, mais alors on fait diminuer la dernière parenthèse liée au débit passant dans l’éolienne. Un calcul d’optimisation (pour les aficionados, une simple calcul d’extremum en dérivant par rapport à ![]() ), montre alors que l’optimal est de diviser la vitesse par 3, c’est-à-dire
), montre alors que l’optimal est de diviser la vitesse par 3, c’est-à-dire ![]() . Si on remplace cette valeur optimale de ralentissement de l’air dans la puissance récupérée, on obtient
. Si on remplace cette valeur optimale de ralentissement de l’air dans la puissance récupérée, on obtient
![]()
On voit que dans le meilleur des cas on ne pourra récupérer que 16/27 de la puissance du vent, jamais plus, ce qui fait environ 59%. Cette limite théorique au rendement d’une éolienne s’appelle la limite de Betz, du nom d’un pionnier Allemand des technologies éoliennes. En pratique il faut encore que l’alternateur transforme l’énergie de rotation du rotor en électricité, ce qui diminue le rendement maximal un peu au dessus de 50%.
Dans un vent fort dont la puissance est de 500W/m2, il va donc falloir plutôt un rotor de 160m (au lieu des 115m calculés plus haut si on pouvait tout récupérer) afin de produire 5MW.
Les rendements en pratique
Comparons avec le rendement d’une véritable éolienne, comme par exemple au hasard la Vestas V90 de 3MW de puissance nominale. Voici la puissance produite, ainsi que le rendement de l’éolienne, en fonction de la vitesse du vent :
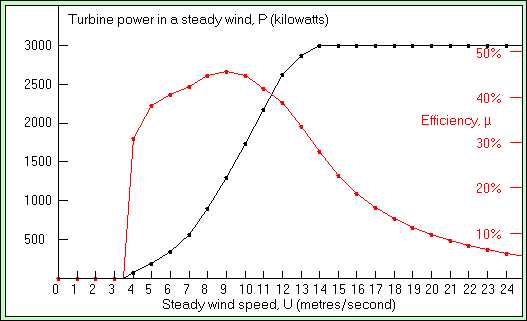
Source : Windpower Program et Vestas.
On s’aperçoit qu’il y a trois régimes. Tout d’abord pour des vitesses trop faibles (inférieures à 3m/s) on ne récupère rien, alors même que la puissance disponible est déjà très faible puisqu’elle va comme le cube de la vitesse. Il ne sert en effet à rien de concevoir une éolienne optimale pour ces faibles vitesses. Ensuite pour des vitesses intermédiaires on a des rendements tout-à-fait honorables puisqu’on récupère un peu plus de 40% de l’énergie du vent (on voit même que cela peut aller jusqu’à 45%), et la puissance reçue augmente bien comme le cube de la vitesse. Puis pour de forts vents, l’éolienne sature et sa puissance n’augmente plus, si bien que son rendement chute. L’éolienne n’est pas non plus conçue pour tirer profit de ces vents forts peu fréquents. Le vent est si rapide que les pales sont des vraies passoires !
On observe que des progrès immenses ont été accomplis depuis les moulins à ailes plates, et les éoliennes modernes ont désormais quasiment atteint la limite de Betz puisqu’ils frôlent les 50% d’efficacité. Il n’y a donc que peu d’espoir d’amélioration à espérer de ce côté là. On peut les concevoir plus légères, avec des matériaux moins rares (notamment pour les aimants de l’alternateur), plus résistantes aux vibrations, plus silencieuses, flottantes etc… mais il ne peut en aucun cas y avoir de miracle technologique dans la récupération du vent.
Les grilles d’éoliennes
On a pris coutume d’appeler un groupe d’éoliennes une ferme d’éoliennes. Le nom est vraiment pas terrible puisqu’il consiste à nommer quelque-chose par ce que ça n’est précisément pas. Personnellement, je préfère largement le terme de parc éolien.
La question est de savoir quelle est la quantité d’éoliennes que l’on peut installer sur une surface de terrain donnée, et quelle est la puissance maximale que l’on peut en espérer lorsque le vent souffle à la bonne vitesse. Pour cela, il faut se rendre compte que les éoliennes étant si performantes à extraire l’énergie du vent, elles perturbent très largement l’écoulement de l’air. Si on regarde ce qui se passe derrière l’éolienne, on a de l’air fortement ralenti tandis que sur les côtés, l’air n’a pas été ralenti. Il existe donc une zone où de l’air s’écoulant de manière rapide est très proche d’air relativement lent. Schématiquement l’écoulement de l’air a le profil suivant :
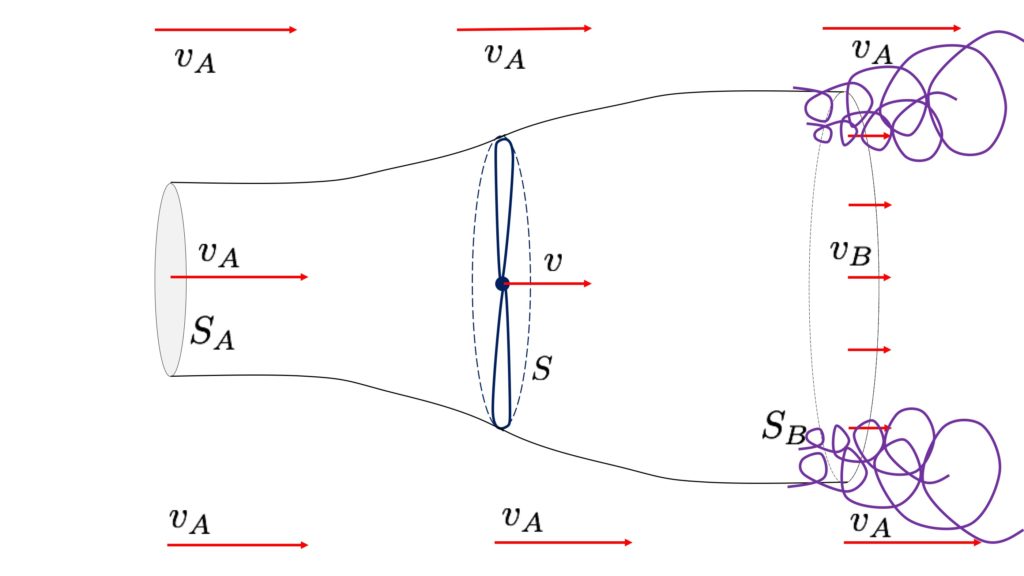
Des tourbillons, c’est-à-dire de la turbulence (pour faire simple, c’est de l’air qui se déplace de manière chaotique dans de multiples directions) vont se développer et perturber le bel écoulement du vent. Le phénomène physique à l’origine de ces turbulences est l’instabilité de Kelvin-Helmoltz qui apparait dès que des fluides ont des vitesses différentes, comme on le voit sur le schéma ci-dessous.
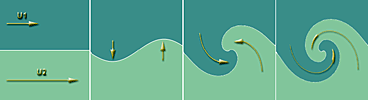
La turbulence est le moyen que trouve le fluide pour mélanger les zones de vitesses différentes. Une fois que tout est bien mélangé, le fluide peut retourner à un écoulement plus ordonné, avec l’essentiel des vitesses dans la même direction, ce qui est la condition nécessaire pour pouvoir faire fonctionner une éolienne. L’agitation associée à la turbulence va par ailleurs se retrouver sous forme de chaleur, c’est-à-dire sous forme d’agitation des molécules, mais cette forme d’énergie ne permet pas de fournir un travail efficace. Au final, on comprend qu’une éolienne ne peut jamais récupérer toute l’énergie du vent, et ce qu’elle n’a pas pu récupérer nous est essentiellement devenu inutile.
Il va donc falloir espacer les éoliennes les unes des autres. Entre une éolienne et la suivante dans la direction du vent, on compte qu’il faut environ 10 fois (certains ne mettent que 7 fois) le diamètre du rotor pour que les turbulences aient bien diminué, et que l’écoulement ait retrouvé à peu près la vitesse initiale en se nourrissant des couches d’air n’ayant pas été ralenties (l’air passé sur les côtés et par dessus l’éolienne ). De plus, lorsqu’elles sont placée les unes à côté des autres (comme par exemple sur une ligne de crête), il faut les espacer d’au moins 5 diamètres de rotor afin de ne pas trop perturber l’écoulement du vent, ce qui nuirait également à l’efficacité. Pour un grand parc d’éoliennes, on va à la fois disposer les éoliennes les unes à côté des autres et les unes derrière les autres. Un parc éolien vu de dessus ressemble donc à la figure suivante, qu’il faut ensuite recopier à l’identique dans toutes les directions pour en faire une grille.
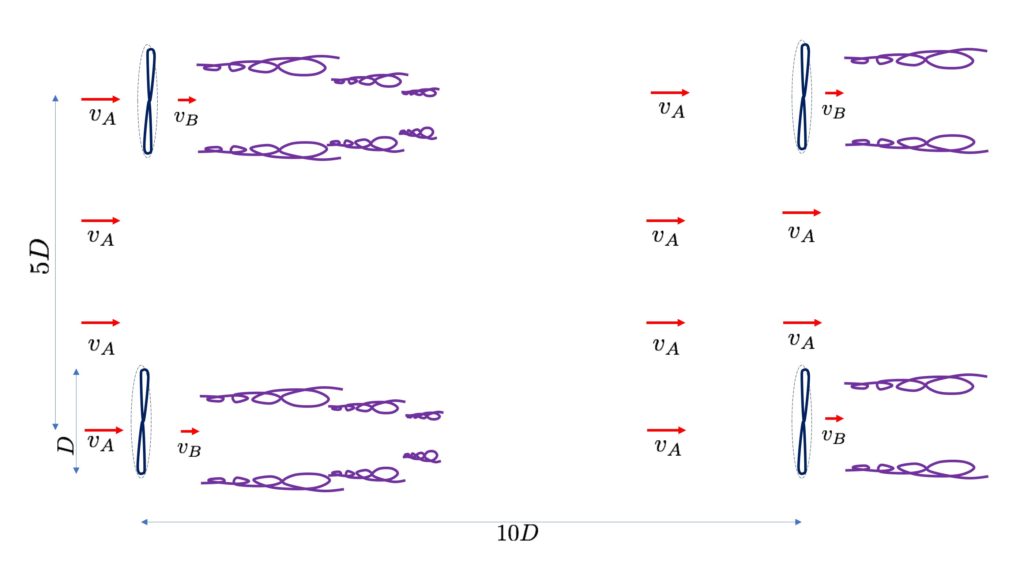
Une conséquence directe est que plus on augmente la taille des éoliennes du parc, donc de leurs rotors, afin de les rendre plus puissantes (plus 200 mètres pour les monstres de 12MW), plus il faut les espacer. La puissance de l’éolienne augmente avec la taille du rotor, puisque le débit de vent est proportionnel à la surface du rotor. Cependant, la densité d’éoliennes, c’est-à-dire le nombre d’éoliennes par unité de surface de terrain, va alors aller comme l’inverse du diamètre du rotor, puisque les espaces sont précisément calculés en multiples de ce diamètre ! Quelle que soit la taille des éoliennes, et pourvu qu’elles soient suffisamment grandes pour capter le vent en hauteur (un peu plus rapide et plus régulier), la puissance installée par surface de terrain sera une constante dépendant essentiellement seulement de la qualité du vent.
Si on regarde les différents parc éoliens sur terre, qu’ils soient avec de nombreuses éoliennes de 2MW, ou de bien moins nombreuses géantes de 8MW, on constate que la puissance installée ne dépasse que rarement 4MW/km2 (je reconnais que ce chiffre au doigt mouillé est assez difficile à obtenir). Pour l’éolien en mer, il est facile d’obtenir les puissances installées par unité de surface car il s’agit toujours de grandes grilles régulières dont l’aire est bien connue, et c’est toujours de l’ordre de 5MW/km2. Par exemple pour le futur parc du Tréport près de Dieppe, nous aurons des éoliennes géantes de 180m de diamètre de 8MW, mais espacées de 1900 mètres dans une direction et 1000 mètres dans l’autre, si bien qu’il y aura un tout petit peu plus d’une demi éolienne par kilomètre carré, et l’installation fournira un peu moins que 5MW/km2. Les autres parcs en mer déjà installés en Allemagne ou au Danemark ont des caractéristiques similaires.
Facteurs de charge et limites
Les éoliennes ne produisent pas toujours, loin s’en faut, puisqu’elles ne peuvent produire que quand le vent souffle à la bonne vitesse. On peut définir le facteur de charge comme étant le temps pendant lequel l’éolienne aurait fonctionné, si elle ne pouvait que soit fonctionner à pleine capacité, soit ne pas fonctionner du tout. On peut l’exprimer soit en heures par an (en se rappelant qu’il y a 8766 heures par an), soit en pourcentage du temps. Pour l’éolien terrestre, les très bon sites dépassent un peu les 25%, i.e. les 2200 heures effectives à pleine puissance. Mais ce facteur de charge ne fait que baisser au fur et à mesure que les sites les plus intéressants ont été équipés. En Allemagne, le facteur de charge est désormais inférieur à 20% pour l’éolien terrestre suite au déploiement massif de parcs. L’éolien en mer, certes plus compliqué à développer, est plus intéressant, avec des facteurs de charge qui peuvent aller jusqu’à 40%. Pour l’éolien terrestre, la production moyenne, une fois pris en compte ce facteur de charge, est donc plutôt de l’ordre de 1MW/km2 voire un peu moins, et autour de 2MW/km2 pour les bons sites d’éolien en mer. Pour pouvoir produire les 500TWh par an d’électricité consommée (soit une production moyenne de (57GW) uniquement avec de l’éolien terrestre, il faudrait environ 57000km2 de terrain très bien venté équipé en éoliennes, soit un peu plus de 10% de la surface de la France. Et si on voulait produire toute l’énergie finale consommée (dont l’électricité n’est qu’un tiers), il en faudrait trois fois plus !
Par ailleurs, une limite liée à cette source d’énergie est son intermittence. En fonction de l’importance de l’éolien dans le mix énergétique, et plus généralement des énergies intermittentes, cela peut être un problème central sans capacités de stockage adéquates ou sans possibilité de lisser la consommation. Et même avec des capacités de stockage, il faut également surdimensionner les réseaux et prévoir une surproduction pour compenser les pertes liées au cycle stockage/réutilisation. C’est donc bien plus que 10% du territoire qu’il faudrait équiper, ce qui implique forcément de devoir utiliser des zones moins bien ventées, rendant alors l’objectif impossible à atteindre.
On rentre alors inévitablement dans un problème encore plus crucial pour le développement de l’éolien à très grande échelle (c’est-à-dire pour couvrir une fraction très importante de la consommation mondiale d’énergie), à savoir que la ressource éolienne globale n’est pas suffisante pour couvrir la totalité des besoins énergétiques. Le développement massif tendrait notamment à modifier les vents de manière globale et in fine à faire plafonner les rendements par surface de terrain.
Si vous avez aimé ce billet, n’hésitez pas à le partager, notamment sur les réseaux sociaux avec les boutons ci-dessous. Et pour recevoir une notification à chaque nouveau billet, vous pouvez vous abonner avec votre adresse mail sur la colonne à droite.
Suivez-moi aussi sur Twitter : @CyrilPitrou
Merci !

C’est très intéressant de comprendre le rendement maximal théorique (et donc la limite globale que l’on peut espérer de la production éolienne).
Je ne suis pas sûr de bien saisir le 5D et le 10D dans le quadrillage. Cela suppose déjà qu’il y a un seul vent dominant et qu’on se cale dessus ? est-ce qu’on ne peut pas imaginer aussi un quadrillage triangulaire ?
On peut disposer les éoliennes différemment en effet. Pour le parc du Tréport, les lignes sont décalées pour avoir un maillage triangulaire, et j’imagine que le but est que l’éolienne juste derrière (pour les vents dominants) soit le plus loin possible. Mais il n’y a pas vraiment de miracle à attendre de ce côté là. En effet pour les grands parcs éoliens, les études théoriques montrent que ce qui compte est la surface de terrain par éolienne. On peut donc tout aussi bien les disposer sur un maillage carré avec un espacement de 7 diamètres, plutôt qu’avec un rectangle de largeur 5 et longueur 10. Pour les très grands parcs, il semblerait qu’il faille également encore diminuer la densité d’éoliennes avec 10 voire 15 diamètres de rotor entre les éoliennes (voire la table 3 de ‘Global available wind energy with physical and energy return on investment constraints, Elise Dupont et al., Applied Energy 209 (2018) 322–338’).
Bonjour Cyril,
bravo et merci pour cet excellent résumé de la problématique du développement massif de l’éolien dans le cadre d’un scenario de développement soutenable. On rencontre des limites analogues pour la collecte de l’énergie solaire : installer beaucoup de modules implique de les incliner moins pour qu’ils ne se fassent pas d’ombre. La limite de ce que l’on peut collecter est l’énergie incidente sur la surface que le capteur ombrage. Si les capacités planétaires sont en effet limitées et le gisement éolien soumis à des rétroactions négatives à son exploitation massive, on peut cependant s’attendre à ce que le foisonnement à l’échelle d’un voire de plusieurs continents interconnectées ( Eurasie, Afrique et Amériques par exemple) permette de réduire notablement les besoins de stockage, surtout si on fait appel au mix éolien-solaire optimal. Ceci à condition de ne pas espérer autre chose que le minimum vital dans les périodes creuses de la production. Les recherches, sur le transport de l’énergie et la gestion des réseaux, sur le stockage et sur les matériaux et procédés devraient permettre de repousser un peu les limites. Nonobstant ces ajustements optimaux, il faudra accepter de réduire fortement la voilure (le facteur quatre sur nos émissions, à force d’avoir reculé depuis bientôt 30 ans sa mise en œuvre est devenu un amuse-bouche à coté des efforts à faire aujourd’hui pour atteindre zéro émission nette en 2050, nous sommes aujourd’hui au pied du mur et, malheureusement, les occidentaux dans leur immense majorité semblent ne pas vouloir changer autrement qu’à la marge). Le temps est venu d’aller vers des sociétés frugales ne gaspillant plus futilement énergie et matière, de consommer l’énergie quand elle est disponible et de stopper la croissance de la population humaine pour sortir enfin de notre statut d’espèce envahissante la seule réellement « nuisible » sur cette planète. La seule capable, tout en vivant pour beaucoup de ses membres dans l’opulence, d’organiser le malheur et l’exclusion d’une fraction importante de ses semblables. Il nous faut urgemment dépasser notre incapacité génétique à raisonner autrement qu’en terme de bénéfices égoïstes immédiats et apprendre enfin à auto-réguler nos désirs sans bornes. Si nous n’en sommes pas capables, toute notre science et notre technologie ne nous permettra pas de repousser les limites planétaires et l’avenir de nos sociétés est bien sombre.
Bravo pour ce blog sur lequel je reviendrai volontiers pour lire d’autres articles. Bien cordiales salutations.
Vincent Bourdin
CNRS – Université de Paris-Saclay
Bonjour, je suis d’accord malheureusement dépasser la génétique est impossible. Je pense que l’ombre des panneaux est tout de même bien moins contraignantes à nos latitudes de 45°
bonjour ,
vous écrivez « Pour pouvoir produire les 500TWh par an d’électricité consommée (soit une production moyenne de (57GW) uniquement avec de l’éolien terrestre, il faudrait environ 57000km2 de terrain très bien venté équipé en éoliennes, soit un peu plus de 10% de la surface de la France. « »
OK : avec une puissance installée de 4 MW/m2 pour l’éolien terrestre soit 230 GW pour 57000 km2 soit une production de 460 TWh pour un fonctionnement annuel moyen de 2 000 h . Mais attention les meilleurs sites sont déjà équipés, « »2000 h » paraît optimiste …
Attention une production s’exprime en GWh et non pas en GW qui est une puissance installée
Vous pensez sérieusement qu’il ne connaît pas la différence entre puissance et énergie?
Bravo pour votre article très bien rédigé et qui met en évidence l’impossibilité de capturer toute l’énergie du vent arrivant sur les pales.
Je ferais juste une remarque, c’est le terme « rendement » qui ne me parait pas adapté. Les valeurs annoncées sont bien faibles ( 95%
Bravo pour votre article très bien rédigé et qui met en évidence l’impossibilité de capturer toute l’énergie du vent arrivant sur les pales.
Je ferais juste une remarque, c’est le terme « rendement » qui ne me parait pas adapté. Les valeurs annoncées sont bien faibles (inférieures à 59%) alors qu’il y a peu de pertes dans une éolienne.
En effet, le rendement est, par définition en physique, égale à la puissance utile en sortie (les KWH électriques) divisé par la puissance absorbée en entrée (celle qui fait tourner les pales), la différence entre ces deux puissances étant dissipée en chaleur. Avec cette définition le rendement d’une éolienne est, comme pour tous les alternateurs de puissance, supérieur à 95%.
La puissance non récupérable par l’éolienne (41% d’après la loi de Betz) n’est pas une puissance perdue dans l’éolienne et qui fait chuter le rendement. C’est une puissance non utilisable. C’est pourquoi le terme efficacité » me parait mieux adapté que le terme « rendement ». J’intitulerais votre article « Efficacité théorique d’une éolienne » plutôt que « Rendement théorique d’une éolienne »
L’efficacité d’une éolienne ne peut pas dépasser 59%
Le rendement est supérieur à 95%